Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 6.Problemas - Ex. 189

A viga é composta por quatro peças de madeira coladas, como mostra a figura. Se o momento fletor interno for M   =   120   k N . m , determine a tensão de flexão máxima na viga. Trace um rascunho tridimensional da distribuição de tensão que age na seção transversal.

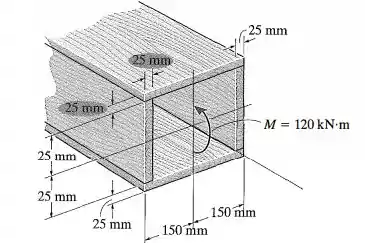
Passo 1

Primeiro, vamos fazer o DCL:

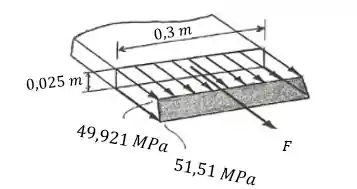
Passo 2

Com isso, vamos calcular o momento de inercia para depois encontrarmos as tensões de flexão:

I = 0,3 × 0,03 3 12 - 0,25 × 0,025 3 12 = 3,4948 × 10 - 4   m 4

Para σ m á x :

σ m á x = M C I = 120 × 10 3 × 0,15 3,4948 × 10 - 4        

σ m á x = 51,51   M P a

Para σ m i n :

σ m i n = M y I

σ m i n = 120 × 10 3 × 0,125 3,4948 × 10 - 4

σ m i n = 49,921   M P a

Passo 3

Por fim, temos que a força resultante é dada por:

F = 51,51 + 49,921 × 10 6 0,025 0,3 2 F = 354,10   k N

Resposta

F = 354,10   k N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Hastes retas com 0,3 0 i n de diâmetro e 200 f t de comprimento são utilizadas algumas vezes para desobstruir dutos enterrados ou para passar cabos em dutos novos. As hastes são feitas de aço de alta
Utilizando a tensão admissível de 120M p a , determine o maior conjugado M que pode ser aplicado à viga cuja seção transversal é a mostrada.Resolva a parte a, admitindo que a seção transversal da viga
Sabendo que, para a viga mostrada na figura a tensão admissível é de 82,7M P a em tração e de 110,3M p a em compressão, determine o maior momento fletor M que lhe pode ser aplicado.
Sabendo que, para a viga extrudada mostrada na figura, a tensão admissível é de 120 M P a em tração e de 150M P a em compressão, determine o maior momento fletor M que lhe pode ser aplicado.
Resolva o P r o b l e m a 4.16 considerando que d = 40 m m .