Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 1.Problemas - Ex. 77

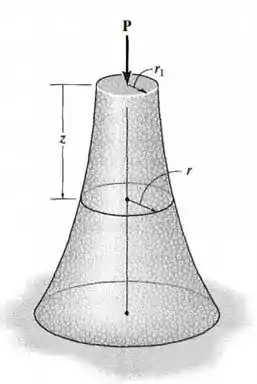
O pedestal suporta uma carga P em seu centro. Se a densidade de massa do material for ρ , determine a dimensão radial r em função de z   de modo que a tensão normal média no pedestal permaneça constante. A seção transversal é circular.

Passo 1

Desejamos encontrar o valor de r mostrado na figura estando em função de z de tal forma que a tensão normal média ( σ m e d ) permaneça constante, dado que a seção transversal é circular.

Passo 2

Podemos definir para esse caso as seguintes formas de obter a tensão

σ = P + w 1 A   e   σ = P + w 1 + d w A + d A

Igualando-se esses dois ( σ ) vamos obter

P ⋅ d A + w 1 ⋅ d A = A ⋅ d w

d A ⋅ P + w 1 = A ⋅ d w

d w d A = P + w 1 A = σ   ( i )

Onde

d A = 2 π r ⋅ d r

d w = π r 2 ⋅ ρ ⋅ g ⋅ d z

Substituindo em ( i ) teremos

π r 2 ⋅ ρ ⋅ g ⋅ d z 2 π r ⋅ d r = σ

r ⋅ ρ ⋅ g ⋅ d z 2 ⋅ d r = σ

Temos, assim, uma equação diferencial separável que podemos fazer

ρ ⋅ g 2 ⋅ σ ⋅ ∫ 0 z d z = ∫ r 1 r 1 r   d r

ρ ⋅ g ⋅ z 2 ⋅ σ = ln ⁡ ( r r 1 ) → r = r 1 ⋅ e ρ ⋅ g ⋅ z 2 ⋅ σ   ( i i )

Passo 3

Nossa tensão normal é dada por

σ = P π ⋅ r 1 2

Assim, podemos substituir em ( i i ) e obteremos

r = r 1 ⋅ e ρ ⋅ π r 1 2 ⋅ z 2 ⋅ P

Resposta

r = r 1 ⋅ e ρ ⋅ π r 1 2 ⋅ z 2 ⋅ P

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A prancha de madeira está sujeita a uma força de tração de 425N . Determine a tensão de cisalhamento média e a tensão normal média desenvolvidas nas fibras da madeira orientadas ao longo da seção a -
Os dois elementos de aço estão interligados por uma solda de topo angular de 60°. Determine a tensão de cisalhamento média e a tensão normal média suportada no plano da solda.
A estrutura de dois elementos está sujeita a um carregamento distribuído mostrado. Determine a tensão normal média e a tensão de cisalhamento média que agem nas seções a - a e b - b . A seção transver
A barra tem área de seção transversal A e está submetida à carga axial P . Detetmine a tensão normal média e a tensão de cisalhamento média que agem na seção sombreada que está orientada a um ângulo θ
A lança tem peso uniforme de 3k N e é alçada até a posição desejada por meio do cabo B C . Se o cabo tiver diâmetro de 15m m , construa um gráfico da tensão normal média no cabo em função da posição d