Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 7.Problemas - Ex. 89

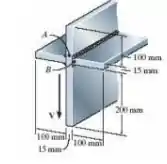
A viga é composta por três chapas finas soldadas, como mostra a figura. Se submetida a um cisalhamento V = 48 kN, determine o fluxo de cisalhamento nos pontos A e B. Calcule também a tensão de cisalhamento máxima na viga.

Passo 1

Oi oi, meu xuxuzinho!! Tudo bem com você?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos diz que tem essa viga tem uma esse formato estranho, e nos pede o fluxo de cisalhamento em cada um daqueles pontinhos ali e a tensão de cisalhamento máxima. Partiu??

Passo 2

Ok, nós vamos começar pensando na barra. Antes de mais nada, vamos calcular nosso centroide da seção transversal.

y =   ∑ A   y   ∑ A =   3 15   x   15 ) ( 15 7,5 + 2 1 00   x   15 2 0 7,5 3 15   x   15 + ( 2 100   x   15 ) = 176,917   m m

Agora que já sabemos disso, podemos calcular nosso I.

I =   0,015 x   0,03 15 3 12 + 0,3 15   x   0,015   x   0 , 0194 2 + 2   0 , 1   x   0 , 0 15 3 12 + 0,1   x   0,015   x   0,0305 8 2 = 4,37135   x   10 - 5   m 4

Pronto, com o nosso momento de inércia calculado, vamos achar os nossos Qs.

Q a = A a ' y a ' = 0,1   x   0,015 0,2 15 - 0 , 17692 + 0,05 = 1,321245   x   10 - 4   m 3    

Q b = A b ' y b ' = 0,1   x   0,015 0,2 0 75 - 0 , 17692 = 4,58745   x   10 - 5   m 3

Q m a x = A ' y ' = 0,1 76917   x   0,015 0 , 0884585 = 2,34747   x   10 - 4   m 3

Passo 3

Pronto!! Agora vamos jogar tudo lá na nossa formulinha e teremos a nossa tensão de cisalhamento e, consequentemente, o nosso cortante.

q = V Q 2 I

q a = V Q I = 145   k N / m

q b = V Q I = 50,4   k N / m

τ m a x = V Q I t = 17,2   M P a

Resposta

q a = 145   k N / m

q b = 50,4   k N / m

τ m a x = 17,2   M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A viga é composta por quatro tábuas coladas ao longo das linhas de junção. Se a cola puder resistir a 15 kN/m, qual é o cisalhamento vertical máximo V que a viga pode suportar?
O elemento está sujeito a uma força de cisalhamento V = 2 kN. Determine o fluxo de cisalhamento máximo no elemento. Todos os segmentos da seção transversal têm 15 mm de espessura.
Uma chapa de aço com espessura 6 mm é dobrada para formar a seção de paredes finas mostrada na figura. Se for submetida a uma força de cisalhamento V = 1,25 kN, determine a tensão de cisalhamento no p
O elemento está sujeito a uma força de cisalhamento V = 2 kN. Determine o fluxo de cisalhamento nos pontos A, B e C. A espessura de cada segmento de paredes finas é 15 mm.