Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 7.Problemas - Ex. 88
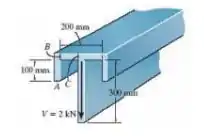
O elemento está sujeito a uma força de cisalhamento V = 2 kN. Determine o fluxo de cisalhamento máximo no elemento. Todos os segmentos da seção transversal têm 15 mm de espessura.
Passo 1
Oi oi, meu xuxuzinho!! Tudo bem com você?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos diz que tem essa viga que tem esse formato estranho, e nos pede o fluxo de cisalhamento máximo.
O fluxo de cisalhamento é dado por
é cortante sobre essa seção; o momento estático; o momento de inércia.
Maaas, quem é o fluxo de cisalhamento máximo?? Cara, ele é o fluxo que ocorre no eixo neutro da nossa seção. Esse eixo passa pelo centroide da seção. Então basicamente, vamos calcular na linha que passa pelo centroide dessa seção diferentona.
Partiu??
Passo 2
Ok, nós vamos começar pensando na barra. Antes de mais nada, vamos calcular nosso centroide da seção transversal.
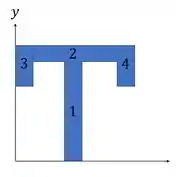
Repara que e tem a mesma área e a mesma coordenada de centroide, então a gente calcula as coisinhas só para o 3 e multiplica por 2.
Agora que já sabemos disso, podemos calcular nosso I. Vamos usar o teorema dos eixos paralelos
Passo 3
Viu que descobrimos o centroide, né? Agora a gente sabe onde vamos calcular o fluxo . Só falta calcularmos com relação a linha que passa por esse centroide.
Esse vai ser o nosso máximo.
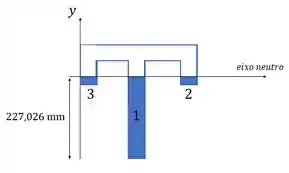
Vamos calcular em relação a área abaixo do eixo neutro (que passa pelo centroide), porque é mais simples que calcular pela área da seção acima, beeleza?
Podemos calcular o assim:
De novo podemos usar que e tem as mesmas propriedades:
Passo 4
Pronto!! Agora vamos jogar tudo lá na nossa formulinha e teremos o nosso fluxo de cisalhamento máximo. Lembrando que :