Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 13.Problemas - Ex. 26
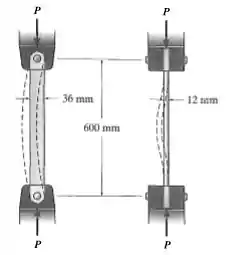
26. As extremidades do elo de aço-ferramenta de uma máquina de forjar estão acopladas aos garfos por pinos, como mostra a figura. Determine a carga máxima que ele pode suportar sem sofrer flambagem. Use um fator de segurança para a flambagem. Observe que, no lado esquerdo da figura, as extremidades estão presas por pino, ao passo que no lado direito, elas estão engastadas
Passo 1
Primeiro, vamos calcular a força crítica para o caso do lado esquerdo pela fórmula:
Como as extremidades estão presas por pinos, temos .
O momento de inércia no eixo , como é uma seção retangular, é dado pela fórmula:
Onde é a aresta paralela ao eixo e é a aresta perpendicular ao eixo.
E temos, também, por ser dado no enunciado que é um aço :
Passo 2
Vamos calcular a tensão devido à força crítica para verificar se ele ultrapassa a tensão de escoamento :
Como , a carga crítica é admissível elemento.
Passo 3
Agora que a gente já tem a força crítica e o fator de segurança, vamos calcular carga máxima que o elemento sofre sem sofrer flambagem:
Passo 4
Como já calculamos a carga para o caso do lado esquerdo, vamos achar a carga para o caso do lado direito.
A diferença desse caso para o outro é o momento de inércia e o
Como as extremidades estão engastadas, .
Já o momento de inércia será:
Passo 5
Calcularemos a tensão devido à força crítica nesse caso para ver se ela excede a tensão de escoamento:
Como , a carga crítica é admissível elemento.
Passo 6
E por fim, vamos calcular carga máxima que o elemento sofre sem sofrer flambagem pelo fator de segurança:
Resposta
Como a carga máxima admissível encontrada para o segundo caso, a resposta será essa: