Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 6.Problemas - Ex. 182

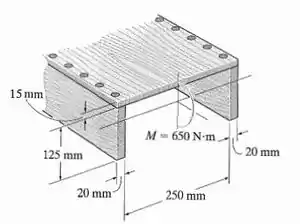
A viga é composta por três tábuas unidas por pregos, como mostra a figura. Se o momento que age na seção transversal for M   =   650   N . m , determine a força resultante que a tensão de flexão produz na tábua de cima.

Passo 1

Fala aí galera, vamos para mais uma resolução para você ficar craque nessa matéria. Este problema é simples e pequeno, só temos que ter atenção. Primeiramente, vamos fazer o Diagrama do Corpo Livre:

Passo 2

Agora, temos que encontrar o centroide da seção transversal para esta tábua. Sua fórmula é dada por:

y C G = ∑ A y C G   ∑ A

y C G = 2 20 × 125 62,5 + 290 × 15 132,5 2 20 × 125 + 290 × 15

y C G = 95,067  

Passo 3

Com isso, vamos encontrar o momento de inércia, dado por:

I = 2 0,02 × 0,125 3 12 + 0,02 × 0,125 × 0,095067 - 0,0625 2 + 0,290 × 0,015 3 12 + 0,290 × 0,015 × 0,1325 - 0,095067 2 I = 1,8 × 10 - 5 m 4

Passo 4

Por fim, temos que encontrar as tensão máxima e mínima na tábua a fim de obtermos a força resultante que estas tensões produzem na tábua. Para σ m á x , temos:

σ m á x = M c I

σ m á x = 650 0,140 - 0,095067 1,8 × 10 - 5 σ m á x = 1,623   M P a

E para σ m i n :  

σ m í n = M c I

σ m í n = 650 0,125 - 0,095067 1,8 × 10 - 5 σ m í n = 1,081   M P a

Sabendo que a força resultante deve ser aplicada na área da tábua, para a F R concentrada, temos:

F R = 1,6234 + 1,0815 10 6 0,015 0,290 2 F R = 5,88   k N

Resposta

F R = 5,88   k N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma barra retangular é feita de um material para o qual o modulo de elasticidade é E t em tração e E c em compressão. Mostre que a curvatura da barra em flexão pura é 1 ρ = M E r I Em que: E r = 4 E t
Sabendo que M = 250N m , determine a tensão máxima na barra mostrada quando o raio r dos adoçamentos é:4mm8mm
sabendo que a tensão admissível para a viga mostrada é de 90M p a , determine o momento fletor M admissível quando o raio r dos adoçamentos é:8mm12mm
Ranhuras semicirculares de raio r devem ser fresadas nos lados de uma barra de aço, conforme mostra a figura. Usando uma tensão admissível de 8 k s i , determine o maior momento fletor que pode ser ap
Ranhuras semicirculares de raio r devem ser fresadas nos lados de uma barra de aço, conforme mostra a figura. Sabendo que M = 4k i p ∙ i n , determine a tensão máxima na barra quando o raio r das ranh