Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 5.Problemas de Revisão - Ex. 162
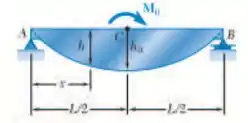
A viga AB, consistindo em uma placa de alumínio de espessura uniforme b e comprimento L, suporta a carga mostrada. (a) sabendo que a viga tem resistência constante, expressa h em termos de no intervalo AC da viga, (b) determine a carga admissível máxima
Passo 1
E ai gurizada tudo belezinha? O enunciado pede que a gente determine a expressão h em termos de no intervalo AC da viga, e a carga admissível máxima
Passo 2
Considerando os valores dos momentos abaixo, vamos realizar o esboço do diagrama de corpo livre ;)
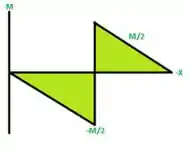
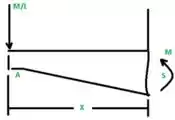
Então vamos começar calculando o momento em J vem comigo :D
Para um seção retangular transversal,
Igualando,
Em
Passo 3
- Resolvendo para
Resposta
Exercícios de Livros Relacionados
Para a viga e o carregamento mostrados, determine a tensão normal máxima provocada pelo momento fletor na seção transversal C .
Para a viga e o carregamento mostrados, determine a tensão normal máxima provocada pelo momento fletor na seção transversal C .
Para a viga e o carregamento mostrados, determine a tensão normal máxima provocada pelo momento fletor na seção transversal C .
Trace os diagramas de força cortante e momento fletor para a viga e carregamento mostrados na figura, e determine a tensão normal máxima gerada pelo momento fletor.
Considerando que a reação do solo é uniformemente distribuída, trace os diagramas de força cortante e o momento fletor para a viga e carregamento mostrados, e determine o valor máximo absoluto ( a ) d