Passo 1
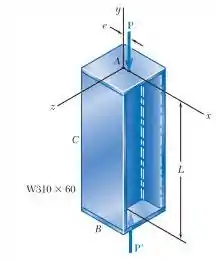
E ai gurizada tudo bem? O enunciado pede que a gente determine (a) a carga P para a qual deflexão horizontal do ponto médio C da coluna é de 15mm, (b) a correspondente tensão máxima na coluna, da seção:
Passo 2
Carga crítica:
Passo 3
- Carga P:
- Tensão normal máxima