Uma viga extrudada tem seção transversal como mostrado e uma espessura uniforme da parede de 4 mm. Para uma força cortante vertical de 12 kN, determinar a tensão de cisalhamento nos quatro pontos indicados e esboçar o fluxo de cisalhamento na seção transversal.
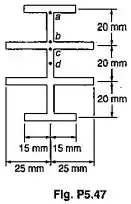
Passo 1
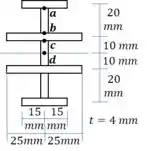
Como a viga é simétrica, já sabemos que o centroide é centralizado!
Então vamos calcular o momento de inércia
Passo 2
Show!
Agora a gente tem que determinar o momento estático em cada um dos pontos de interesse
Para o ponto :
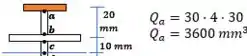
Para o ponto :
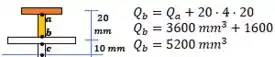
Para o ponto :
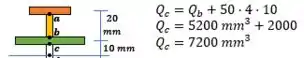
Para o ponto
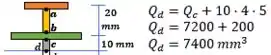
Passo 3
E agora é só calcular as tensões em cada ponto: