Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 6.Problemas - Ex. 29
A viga de madeira mostrada na figura está submetida a uma força cortante vertical de 5,34 kN. Sabendo que a força cortante admissível nos pregos é 333,6 N, determine o maior espaçamento possível s dos pregos.
Passo 1
Beleza! Para encontrar o maior espaçamento s entre os pregos, precisamos encontrar o fluxo de cisalhamento que ocorre na seção, pois a força cortante admissível em cada prego pode ser escrita como:
Em que q é o fluxo de cisalhamento e s é o espaçamento entre os pregos. Só que, para encontrar o fluxo de cisalhamento, que por sua vez é dado por:
Precisamos encontrar o momento de inércia I e o momento de área Q da seção, o V o enunciado já nos deu, que é a força cortante de 5,34 kN a que a viga está submetida. Beleza! Nós sabemos que o momento de área Q é dado por:
Agora observe que o momento de área é dependente da área de estudo (claro!), e observando o problema, vemos que os pregos são colocados na extremidade da viga, então vamos precisar calcular o momento de área dessa seção.
Falta só mais um detalhe! Vamos dividir a seção transversal na barra vertical maior e nas áreas laterais menores, e usando o teorema dos eixos paralelos, vamos encontrar o momento de inércia delas, para encontrar o momento de inércia total da seção.
Passo 2
Ufa! Depois de tudo isso, vamos começar de vez! Vamos começar separando a seção transversal em 5 partes, da seguinte forma:
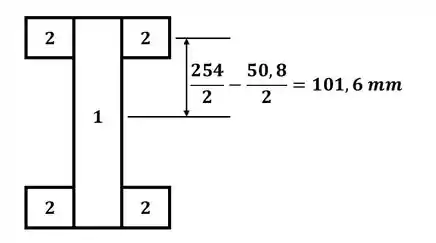
Opa! Já colocamos a distância do centroide da seção 2 com relação ao centroide da seção como um todo, e referência do nosso sistema de coordenadas. Observe que não precisamos separar a seção em 5 seções diferentes, pois as extremidades possuem todas a mesma área e a mesma distância com relação ao centroide da seção completa. Então vamos lá! Como temos somente seções transversais retangulares, o momento de inércia é dado por:
Vamos começar calculando o momento de inércia da seção 1, que será dado por:
Agora para as seções número 2, precisamos usar o teorema dos eixos paralelos, pois o centroide delas está deslocado com relação ao centroide da seção. Então, a equação para o momento de inércia de 2 será:
Com esses dois valores, conseguimos encontrar o momento de inércia da seção, que será dado por:
Passo 3
Agora vamos calcular o momento de área Q da nossa seção 2, que será dado por:
Substituindo os valores conhecidos, temos:
Agora temos todos os valores que precisamos para a equação do fluxo de cisalhamento, então teremos:
Então, agora podemos usar a equação para a força cortante admissível para os pregos, dada por:
Isolando o espaçamento s dessa equação e substituindo os valores conhecidos, temos:
É isso aí! Acabamos por aqui!