Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 5.Problemas - Ex. 10

Para a viga com carregamento indicado, considerar a seção n-n e determinar: (a) a maior tensão normal; (b) a tensão de cisalhamento no ponto a; (c) a maior tensão de cisalhamento.

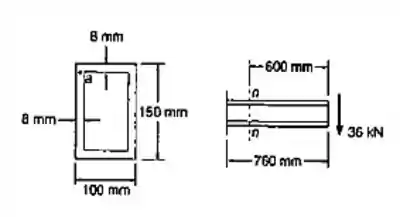
Passo 1

Primeiramente para o cálculo da área, vamos separar nas regições verdese vermelhas.

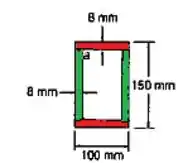
Teremos então

A = 0,1 × 0,008 × 2 v e r m e l h o + 2 × 0,134 × 0,008 v e r d e = 3,744 × 10 - 3 m 2

Passo 2

Onde teremos para o momento de inércia

I z z = Σ I i + A i d i 2

I = 1 12 × 0,1 × 0,15 3 - 1 12 × 0,084 × 0,134 3 = 1,128 × 10 - 5 m 4

Passo 3

a) Para descobrirmos a maior tensão normal fazemos

φ = M c I

Vamos precisar calcular o momento antes que nos vai ser dado por

M = 36 × 10 3 × 600 × 10 - 3 = 21,6   k N

Podemos então agora aplicar a fórmula

φ = M c I = 21,6 × 10 3 × 0,075 1,128 × 10 - 5 = 143,617   M P a

Passo 4

b) Para descobrirmos a tensão de cisalhamento no ponto a

τ = V Q I t

Para isso vamos precisar do Q que nos é dado por

Q = A × y = 0,1 × 0,008 × 0,071 = 5,68 × 10 - 5 m 3

Podemos então aplicarmos a fórmula

τ = V Q I t = 36 , × 10 3 × 5,68 × 10 - 5 1,128 × 10 - 5 × 0,008 × 2 = 11,33   M P a

Passo 5

c) Por último a questão nos pede a maior tensão de cisalhamento

Para isso vamos precisar montar a tabelinha como foi visto na teoria desse tópico

O y -   é dado por

y - = Σ y - A Σ A = 9,2715 × 10 - 5 1,872 × 10 - 3 = 49,527   m m

O que vai ser recalculado e fica

Q = 1,872 × 10 - 3 × 49,527 × 10 - 3 = 9,2715 × 10 - 5 m 3

Então a tensão de cisalhamento fica

τ = V Q I t = 36 , × 10 3 × 9,2715 × 10 - 5 1,128 × 10 - 5 × 0,008 × 2 = 18,494   M P a

Resposta

a )   φ = 143,617

b )   τ a = 11,33   M P a

c )   τ m a x = 18,494   M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a localização e do centro de cisalhamento (ponto O) para o elemento de paredes finas que tem a seção transversal mostrada na figura. Os segmentos do elemento têm a mesma espessura t .
Determine a posição e para a aplicação da força P de modo que a viga sofra deflexão para baixo sem torção. Considere h = 200m m .
Determine a localização e do centro de cisalhamento (ponto O) para o tubo que tem uma fenda ao longo de seu comprimento
Determine a localização e do centro de cisalhamento (ponto O) para o elemento de paredes finas que tem a seção transversal mostrada na figura.
A força P é aplicada à alma da viga como mostra a figura. Se e = 250 m m , determine a altura h da aba direita de modo que a viga sofra deflexão para baixo sem torção. Os segmentos do elemento têm a m