Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 9.Problemas - Ex. 110
Para a viga prismática e o carregamento mostrados nas figuras, determine (a) a inclinação na extremidade A e (b) a deflexão no centro C da viga.
Passo 1
Opaa! Fala pessoal, beleza? Bora pra mais um?! Para resolver esse exercício, vamos utilizar o método do momento de área. Para isso vamos precisar desenhar o diagrama M/EI para a viga. Depois disso, sabemos que a área entre dois pontos sob a curva M/EI representa a inclinação entre esses dois pontos. E para obter a deflexão, vamos utilizar o teorema do segundo momento de área, que nos fornece o desvio tangencial entre dois pontos. Sabendo disso, temos tudo o que precisamos para resolver o exercício, então bora lá!
Passo 2
Beleza, para esse DCL, teremos momento ao longo de toda a viga, só que, como temos duas forças localizadas a mesma distância dos apoios, teremos momento crescente de zero no apoio até um momento máximo nesses pontos, depois disso teremos um momento constante na seção central da viga, entre os pontos B. Devido a simetria do carregamento, sabemos que as reações nos apoios serão iguais e devem ser então metade das forças P, ou seja:
E, o momento equivalente na viga será dado por:
Com , ou com mesma intensidade e direção oposta do outro lado da viga. Sendo assim, vamos calcular o momento na seção central da viga, onde teremos:
Então a nossa parcela para a seção central entre B e D será:
Passo 3
Então, o nosso diagrama será:
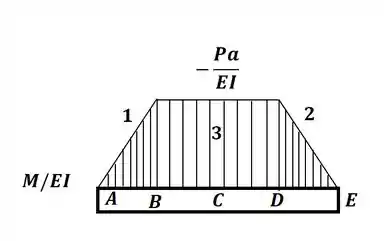
Então, agora vamos calcular as áreas que encontramos e os seus centroides, só lembrando que vamos precisar somente da área entre os pontos AB e entre BC, então teremos:
Tá legal! Agora podemos calcular a inclinação no ponto A, sabendo que a inclinação entre dois pontos é representada pela área sob a curva do diagrama , então a inclinação do ponto A será:
Substituindo os valores encontrados para a área e sabendo que no ponto C não teremos inclinação devido ao carregamento simétrico, teremos:
Beleza, vamos pra (b) agora!
Passo 4
Beleeeza! Agora, sabemos que a deflexão entre dois pontos será dada através do teorema do segundo momento de área, que é dado por:
Em que é a área embaixo da curva e é a distância do centroide da área até o eixo vertical que passa pelo ponto de interesse, que no nosso caso é o ponto C. Então, utilizando as áreas que temos no nosso diagrama , teremos:
Sabendo que não temos deflexão em A devido ao apoio e substituindo os valores conhecidos, teremos:
Shooow!! Terminamos mais um, valeeu!