Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 9.Problemas - Ex. 101
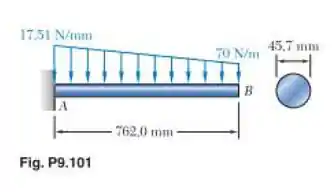
Para a viga uniforme em balanço e o carregamento mostrados na figura, determine (a) a inclinação e (b) a deflexão no ponto B. Use E = 200 GPa.
Passo 1
Opaa! Fala pessoal, beleza? Bora pra mais um?! Para resolver esse exercício, vamos utilizar o método do momento de área. Para isso vamos precisar desenhar o diagrama M/EI para a viga. Depois disso, sabemos que a área entre dois pontos sob a curva M/EI representa a inclinação entre esses dois pontos. E para obter a deflexão, vamos utilizar o teorema do segundo momento de área, que nos fornece o desvio tangencial entre dois pontos. Sabendo disso, temos tudo o que precisamos para resolver o exercício, então bora lá! (Obs: observe que os valores entre as extremidades do carregamento estão muito distantes, então vamos considerar o maior carregamento como 175,1 N/m).
Passo 2
Tá legal! Vamos começar esse exercício desenhando o DCL para a viga como um todo, que será dado por:
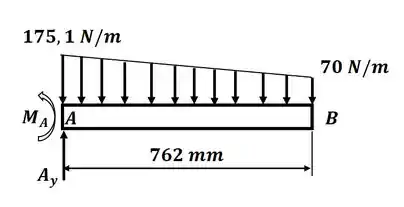
Agora, aplicando o somatório de momentos em relação ao ponto A, teremos:
Agora, aplicando o somatório de forças na direção y, teremos:
Beleza! Agora vamos desenhar o DCL para uma seção da viga de comprimento a partir do ponto A, onde teremos:
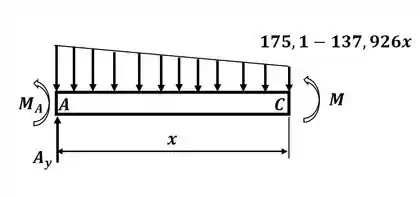
Agora nós vamos aplicar o somatório de momento em relação ao ponto C para encontrar uma expressão para o momento resultante na viga nessa seção. Então, sabendo que a equação da reta de decaimento do momento é dada por:
Teremos:
Passo 3
Então, para a letra (a), temos que a inclinação na extremidade livre, será a inclinação entre os pontos A e B, que nada mais é do que a área abaixo da curva , ou seja:
Devido a função momento encontrada ser complexa, vamos encontrar a área embaixo da curva através da integral do momento, então teremos:
Como temos um engaste no ponto A, não teremos inclinação nesse ponto, e resolvendo a integral, teremos:
Antes de substituir os intervalos de integração, vamos calcular o momento de inércia para a seção. Como temos uma seção circular, o momento de inércia será:
Agora, sim, substituindo os intervalos de integração e os valores conhecidos na equação acima, teremos:
Passo 4
Beleeeza! Agora, sabemos que a deflexão entre dois pontos será dada através do teorema do segundo momento de área, que é dado por:
Em que é a área embaixo da curva e é a distância do centroide da área até o eixo vertical que passa pelo ponto de interesse, que no nosso caso é o ponto B. Então, utilizando novamente o conceito de integral, sabendo que o centroide é dado por:
A equação acima se torna:
Então, substituindo a expressão conhecida para M, teremos:
Resolvendo a integral, teremos:
Substituindo os intervalos de integração e os valores conhecidos de E e I, teremos:
Shooow!! Terminamos mais um, valeeu!