Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 4.Problemas - Ex. 165
Uma viga com a seção transversal mostrada está submetida a um momento , que atua em um plano vertical. Determinar o maior valor permissível do momento fletor , se a máxima tensão na viga não exceder a .
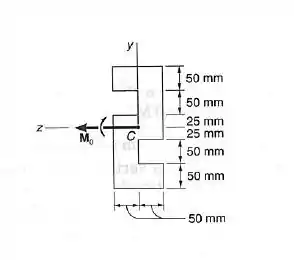
Passo 1
Para achar esse valor de , precisamos primeiro achar os eixos principais de momento de inércia dessa seção. E para isso, a gente precisa achar , e :
Dividindo ela nesses retângulos, a gente pode usar o teorema dos eixos paralelos e calcular:
E para calcular o produto de inércia:
Como os retângulos são simétricos, todos os valem zero. E aí temos:
Passo 2
Agora a gente vai usar o círculo de Mohr para descobrir os momentos de inércia dos eixos principais.
Olha como ficou:
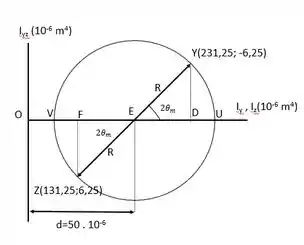
O mais fácil é girar esse segmento no sentido horário, então nosso ângulo vai estar nessa direção e vai valer:
Passo 3
Agora a gente tem que descobrir onde é a linha neutra. Isso porque a tensão máxima ocorre nos pontos mais distantes dela. A gente descobre isso pela fórmulinha:
Onde é o ângulo entre a linha neutra e o eixo . Substituindo os nossos dados:
Nossa linha neutra está nessa posição:
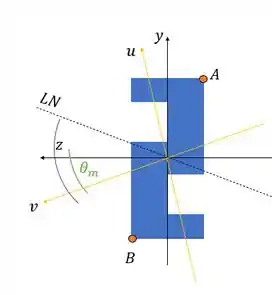
Vemos que os pontos mais distantes da nossa linha neutra são e . Eles terão as tensões máximas.
Passo 4
Vamos usar a relação de tensão no ponto , já que a distância entre a linha neutra e ele é semelhante à distância entre a linha neutra e . Com ela, podemos descobrir o momento máximo. Ela vai ter essa carinha:
Vamos projetar o nosso momento , que está na direção do eixo , nos eixos principais:
E achar e .
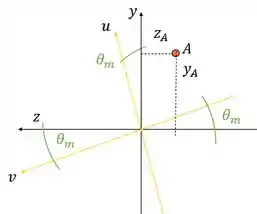
Passo 5
O enunciado diz que:
Como no ponto temos compressão:
Ufa!