Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 4.Problemas - Ex. 174
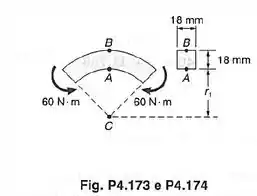
Para a barra curva e o carregamento mostrado, determinar a tensão nos pontos e , quando:
Passo 1
Queremos a tensão em e . Podemos usar a fórmulinha:
Nossos dados são:
- Momento aplicado:
- Raio interno:
- Raio externo:
- Localização do centroide da seção em relação a
- Área da seção:
Agora só falta achar e . Vamos lá!
Passo 2
Como nossa seção é retangular, a gente usa fórmulinha de
Sendo:
Temos que:
E para :
Passo 3
Podemos jogar nossos dados na nossa fórmulinha agora. Fazendo :
Fazendo :
Resposta
Exercícios de Livros Relacionados
Resolva o P r o b l e m a4.121 considerando que as deformações medidas são: ε A = + 600μ eε B = + 420μ
Uma coluna curta em perfil laminada de aço suporta uma placa rígida na qual duas ações PeQ são aplicadas conforme mostrado. As deformações foram medidas nos dois pontos AeB na linha de centro da face
O momento M é aplicado a uma viga com a seção transversal mostrada na figura em um plano formando um ângulo β com a vertical. Determine a tensão no.Ponto A;Ponto B;Ponto D.
O momento M é aplicado a uma viga com a seção transversal mostrada na figura em um plano formando um ângulo β com a vertical. Determine a tensão no.Ponto A;Ponto B;Ponto D.
Uma única força vertical P é aplicada a um poste curto de aço conforme mostrado. Extensômetro localizados em A, B e C indicam as seguintes deformações: ε A = - 500μ eε B = - 1000μ eε C = - 200μ Sabend