Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 5.Problemas - Ex. 86
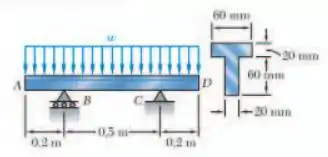
Resolva o problema considerando a seção transversal da viga esteja invertida, com a mesa da viga repousada sobre os suportes em e .
Determine o maior valor admissível de carga distribuída para a viga mostrada, sabendo que a tensão normal admissível é de em tração e de de compressão.
Passo 1
Fala aí, galerinha. Tudo bem com vocês? Bora estudar mecânica e garantir aquele notão na prova.
Como queremos determinar a maior carga admissível, devemos determinar as reações de apoio e encontrar o diagrama. Para isso, vamos esboçar o DCL:
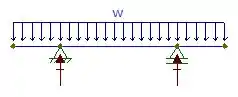
Após o esboço do DCL, vamos utilizar as equações de equilíbrio. Sabemos que:
Por simetria , logo:
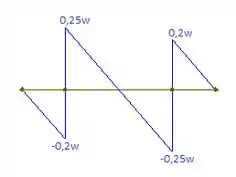
Portanto, podemos esboçar o diagrama de força cortante. Fazendo ele:
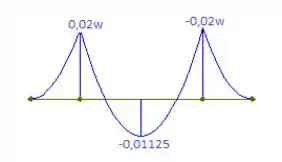
E também, o diagrama de momento:
Agora, vamos determinar a tensão
Passo 2
Agora que temos os diagramas, precisamos determinar o momento de inércia para esta seção. Para isso, temos que determinar o seu centróide. Pelo somatório de momentos de inércia, temos:
Assim, o centróide desta seção vai ser:
E, com isso, o momento de inércia é:
Passo 3
Por fim, sabemos que a tensão pode ser encontrada a partir da seguinte relação:
Com isso, temos uma tensão no segmento e, substituindo:
E pronto! Esta é carga admissível. Bora fazer mais!