Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 6.Problemas - Ex. 81

A viga está sujeita a carga P em seu centro. Determine a distância a dos apoios de modo que a tensão de flexão máxima absoluta na viga seja a maior possível. Qual é essa tensão?

Passo 1

Fala galerinha, tudo certinho? Vamos começar fazendo um DCL da nossa viga:

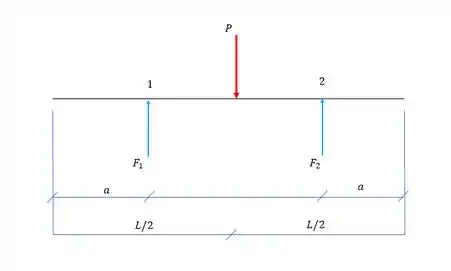
E com isso definimos os pontos 1 e 2 para as aplicações das forças, e aí vamos determinar as reações:

∑ M 1 = 0 → - P L 2 - a + 2 L 2 - a F 2 = 0

F 2 = P L 2 - a 2 L 2 - a

F 2 = P 2

Por simetria, temos que F 1 = F 2 = P 2 , logo, fazendo o diagrama:

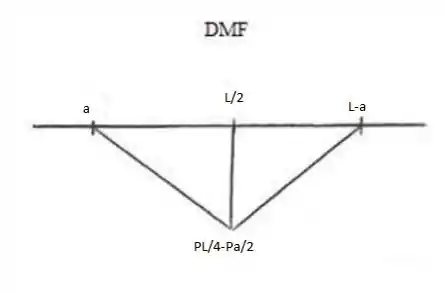
Esse momento pode ser calculado tanto pela esquerda quanto pela direita fazendo:

M m á x = F 2 L 2 - a

M m á x = P 2 L 2 - a

Rearrumando:

M m á x = P L 4 - P a 2

Passo 2

O momento máximo vale P L 4 - P a 2 , logo, a tensão máxima será:

σ m a x = M m á x × c I

Onde:

c = d / 2

E:

I = b d 3 12

Assim:

c I = d 2 b d 3 12

c I = 6 b d 2

σ m á x = P L 4 - P a 2 × 6 b d 2

Passo 3

Analisando a expressão, podemos ver que a tensão é máxima quando a = 0 e esta vale:

σ m á x = P L 4 - 0 × 6 b d 2

σ m á x = 3 P L 2 b d 2

Resposta

a = 0

σ m á x = 3 P L 2 b d 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para o perfil mostrado, determinar o maior momento M que pode ser aplicado, sem que as seguintes tensões admissíveis sejam excedidas: σ a d m = + 40M P a e : σ a d m = - 100M P a .
Um momento de 3,5k N m é aplicado à barra de aço mostrada. Pede-de:Sendo que o momento encurva a barra em torno do eixo horizontal, determinar a máxima tensão e o raio de curvatura;Resolver a parte a)
Sabendo-se que, para a viga extrudada mostrada na figura, a tensão admissível é de 120M P a , à tração, e 15 0M P a à compressão. Determinar o maior momento M que pode ser aplicado.
Para o perfil mostrado, determinar o maior momento M que pode ser aplicado, sem que as seguintes tensões admissíveis sejam excedidas: σ a d m = + 40M P a e σ a d m = - 100M P a .
Sabendo-se que, para a viga extrudada mostrada na figura, a tensão admissível é de 120M P a , à tração, e 15 0M P a à compressão. Determinar o maior momento M que pode ser aplicado.