Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 6.Problemas - Ex. 69

Determine a tensão de flexão máxima absoluta na viga. Cada segmento tem seção transversal

retangular com base de 100   m m e altura de 200   m m .

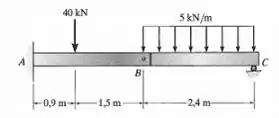
Passo 1

Vamos calcular as reações. Como temos uma rótula em B e sabemos que o momento na rótula deve ser nulo pelos 2 lados, temos:

∑ M b b c = 0 → 2,4 F c - 5 × 24 × 1,2 = 0

F c = 6 k N

∑ F y = 0 → F a + 6 - 52 = 0

F a = - 46 k N

∑ M b a b = 0 → M a + 40 × 1,25 - 2,4 × 46 = 0

M a = 50,4 k N m

Com isso, podemos fazer o diagrama:

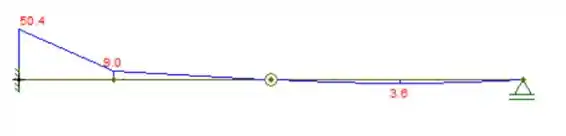
Passo 2

Sabemos que o momento máximo é 50,4kNm. Logo, a tensão máxima será:

σ m a x = 50,4 × 10 3 × 0,1 0,1 × 0,2 3 12 = 75,6 M P a

Resposta

σ m a x = 75,6 M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine as equações da linha elástica para a viga utilizando as coordenadas x 1 e x 3 . Especifique a inclinação em A e o deslocamento no centro do eixo. EI é constante.
A viga é feita de um material com módulo de elasticidade sob compressão diferente do módulo de elasticidade sob tração. Determine a localização c do eixo neutro e deduza uma expressão para a tensão de
Uma tira de aço L 2 com 3m m de espessura e 50m m de largura é curvada até formar um circular de 15m de raio. Determine a tensão de flexão máxima na tira
A figura de um homem executando um salto em altura com vara permitiu estimar por medição que o raio de curvatura mínimo da vara é 4,5 m. Se a vara tiver 40 mm de diâmetro e for feito de plástico refor
Resolva(a) pela fórmula da flexão (b) por integração se o momento M=50N . m for aplicado em torno do eixo y em vez de em torno do eixo x . Aqui, I y=1 / 4π ( 0,04m ) ( 0,08m ) ³ ³.