Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 12.Problemas - Ex. 72

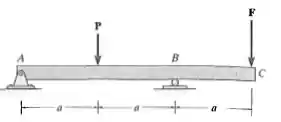
A viga está sujeita à carga P como mostra a figura. Determine o valor da força F que deve ser aplicada na extreimidade da extensão C de modo que a deflexão em C seja nula. EI é constante.

Passo 1

Fala aí pessoal, partiu mais um problema de resmat. Este problema nos pede F . Para encontra-lo, vamos utilizar a função de Macaulay. Primeiro, vamos utilizar as equações de momento e equilíbrio:

∑ M A = 0 - P a - 3 a F + V B = 0 V B = P + 3 F 2

∑ F y = 0 V A + V B - P - F = 0 V A = P - F 2

Passo 2

Pela função de Maculay:

M x = P - F 2 x - P < x - a > 1 + P + 3 F 2 < x - 2 a > 1

Logo, substituindo na equação da linha neutra:

E I d 2 v d x 2 = M x = P - F 2 x - P < x - a > 1 + P + 3 F 2 < x - 2 a > 1

E I d v d x = P - F 4 x ² - P 2 < x - a > 2 + P + 3 F 4 < x - 2 a > 2 + C 1

E I v = P - F 4 x 2 - P 2 < x - a > 2 + P + 3 F 4 < x - 2 a > 3 + C 1 x + C 2

Passo 3

Com isso, temos que as condições de contorno são:

x = 0 → v = 0 x = 2 a → v = 0

Substituindo as condições de contorno na equação da linha elástica, temos: C 1 = 4 F a 2 - 3 P a 2 12

C 2 = 0

Passo 4

Por fim, como a deflexão em C é nula, tem-se:

∆ C = - P - F 45 3 a 3 - P 6 3 a - a 3 + P + 3 F 12 3 a - 2 a 3 + 4 F a 2 - 3 P a 2 12 3 a = 0 F = P 4

Resposta

F = P 4

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para a viga com o carregamento mostrado, determinar:A localização do ponto que ocorre o máximo para a Viga e carregamento do P r o b . 9.4 1 .
Para a viga com o carregamento mostrado, determinar:A intensidade do máximo para a Viga e carregamento do P r o b . 9.41 .
Para a viga com o carregamento mostrado, determinar:A inclinação do ponto A para a Viga e carregamento do P r o b . 9.4 1 .
Para a viga com o carregamento mostrado, determinar:A intensidade do máximo para a Viga e carregamento do P r o b . 9 . 40 .
Para a viga com o carregamento mostrado, determinar:A localização do ponto que ocorre o máximo para a Viga e carregamento do P r o b . 9.4 2 .