Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 12.Problemas - Ex. 55
Determine a inclinação e a deflexão em B. EI é constante.
Passo 1
Fala aí pessoal, partiu mais um problema de resmat. Este problema nos pede as inclinações e a deflexão em C. Para encontra-los, vamos utilizar o método dos momentos de área. Primeiro, devemos encontrar as reações nos apoios através da equação de equílibrio.
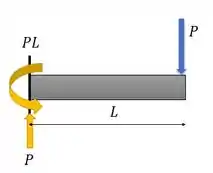
Bora lá!
Passo 2
Nesse método, a gente precisa desenhar o diagram do momento. Como no apoio o momento vale (de acordo com a conenção de sinais para esforços internos) e na ponta vale , podemos marcar esses dois pontos no nosso diagrama.
E repara que nosso carregamento é pontual. Então nosso diagrama vai ser linear, ou seja, podemos ligar esses dois pontos por uma reta e prontinho!
Passo 3
Agora, nós fazemos o diagram , que é basicamente pegar esse diagrama que a gente fez do momento e dividir a função dele por . Já que é uma constante, a cara dele continua linear:
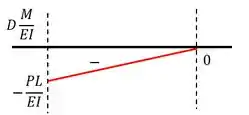
Passo 4
Aí vem o pulo do gato, meu amigo! Para determinar a inclinação e , podemos usar o Teorema 1 do método dos momentos de área. Ele diz que:
Mas repara que , porque isso é um apoio de engaste. E que essa integral aí é a área sob nossa curva do diagrama, que é um triânguo! Então podemos dizer que:
Lembrando que a base desse triângulo é .
Passo 5
E para achar ? Cara, aqui a gente usa o teorema 2 do método dos momentos de área. Ele diz que
Já vimos que essa integral é a área do diagrama . Podemos lembrar também que , porque estamos no apoio. Falta saber quem é .
Cara, ele é o centroide da nossa área desse diagrama aí. Mas atenção: como a gente quer o valor de, precisamos medir o centroide a partir do ponto , tá bem?
Como a área do diagrama é um triângulo, o centroide vai estar em da ponta. Ou seja, em:
E nossa deflexão fica: