Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 12.Problemas - Ex. 48
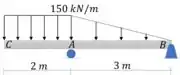
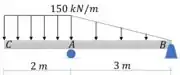
A viga está sujeita à carga mostrada na figura. Determine a equação da linha elástica
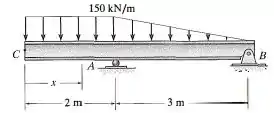
Passo 1
Vamos começar calculando as reações de apoio
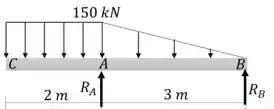
Passo 2
Para que a gente possa utilizar as funções de descontinuidade precisamos que o carregamento contínuo se estenda até o fim da viga. Pode parecer que temos um carregamento contínua em toda a viga, mas se você olhar a tabela 12.2 não verá nenhum carregamento semelhante a este.
Acontece que o que temos nesta viga são dois carregamentos: um carregamento retangular que NÃO chega ao fim da viga. E um carregamento triangular que chega ao fim da viga.
Para que possamos aplicar a tabela 12.2 e as equação de descontinuidade vamos trablhar com a seguinte viga equivalente:
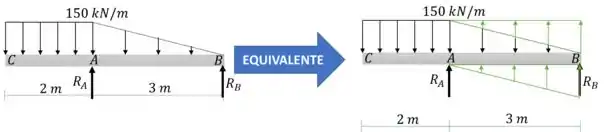
Daqui já definimos a inclinação deste carregamento triangular como:
Passo 3
Pronto, podemos aplicar a tabela 12.2 para gerar uma equação de descontinuidade para o momento fletor.
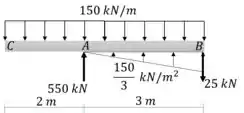
Vamos simplificar as frações. Também sabemos que forças pontuais na extremidade final podem ser ignoradas e que , desde que
Passo 4
Vamos integrar uma vez para ter a equação da inclinação:
Passo 5
Vamos integrar mais uma vez para ter a equação da linha neutra:
Passo 6
Vamos aplicar as condições de contorno para calcular as constantes.
No ponto A temos um apoio. As condições do ponto A são:
Aplicando isso na equação da linha elástica:
Passo 7
No ponto B temos um pino. As condições do ponto B são:
Aplicando isso na equação da linha elástica:
Passo 8
Agora vamos solucionar o sistema linear gerado pelas constantes:
Se subtraírmos a primeira da seguda:
Aplicando então este valor na primeira equação: