Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 9.Problemas de Revisão - Ex. 168

Determine a reação no apoio móvel e desenhe o diagrama de momento fletor para a viga e o carregamento mostrados na figura.

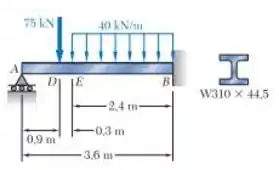
Passo 1

Fala aí, galera. Beleza? Vamos praticar mais mecânica pra tirar aquele 10 na prova.

Esse exercício nos pede para determinarmos a reação no apoio móvel, ou seja, o apoio em A . Para isso, vamos encontrar as equações para momento.

Seja M 1 , o momento gerado pela reação de apoio em A , temos:

M 1 = 3,6 R A

O momento M 2 vai ser o momento resultante da força concentrada que atua no ponto D . Logo

M 2 = - 75 0,3 + 2,4 M 2 = - 202,5   k N ∙ m

E para o terceiro, gerado pela carga distribuída, temos:

M 3 = - 1 2 40 2,4 2 M 3 = - 115,2   k N ∙ m

Agora, vamos esboçar o diagrama M / E I :

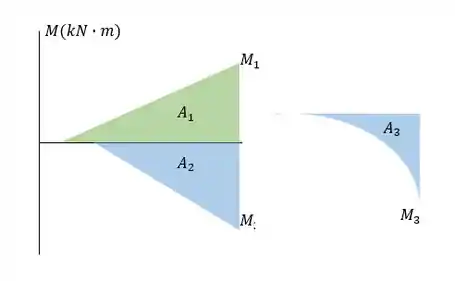
Com isso, vamos calcular cada área do diagrama M / E I . Dividimos ele em três partes, logo:

A 1 = 1 2 3,6 ( 3,6 R A )   A 1 = 6,48 R A

A 2 = 1 2 2,7 - 202,5 A 2 = - 273,375   k N ∙ m 2

A 3 = 1 3 2,4 - 115,2 A 3 = - 92,16   k N ∙ m 2

Passo 2

Em seguida, selecionamos a tangente em B como tangente de referência. Portanto:

θ B = 0 y B = 0

Logo:

y A = t A / B = 0 t A / B = 1 E I 2 3 ∙ 3,6 A 1 + 0,9 + 2 3 ∙ 2,7 A 2 + 0,9 + 00,3 + 3 4 ∙ 2,4 A 3

Para este perfil, o momento de inercia é tabelado, portanto, substituindo:

R A = 65,24   k N

Opa, essa é a reação do apoio móvel.

Passo 3

Por fim, vamos esboçar o diagrama de momento fletor a fim de encontrarmos os momentos nos pontos B e D . Fica assim:

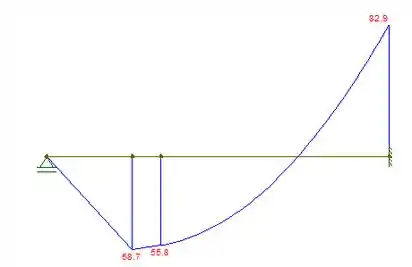
Podemos ver que:

M B = 82,8   k N ∙ m M D = - 58,7 ∙ m

Resposta

R A = 65,24   k N

M B = 82,8   k N ∙ m M D = - 58,7 ∙ m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine as reações nos apoios A e B ; em seguida, trace os diagramas de força cortante e momento fletor. E I é constante. Despreze o efeito da carga axial.
A viga tem E 1 I 1 constante e é suportada pela parede fixa em B e pela haste AC. Se a haste tiver área de seção transversal A 2 e o material tiver módulo de elasticidade E 2 , determine a força na ha
Determine as reações ao momento nos apoios A e B. EI é constante.
Determine as reações nos apoios e, em seguida, trace os diagramas de força cortante e momento fletor. EI é constante.
Determine as reações nos apoios A, B e C; em seguida, trace os diagramas de força cortante e momento fletor.