Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 7.Problemas - Ex. 71
Determine a localização do centro de cisalhamento (ponto O) para o elemento de paredes finas que tem a seção transversal mostrada na figura. Os segmentos do elemento têm a mesma espessura .
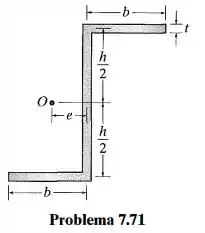
Passo 1
Observe a figura abaixo com o fluxo de cisalhamento sobre a seção. Perceba que por causa da geometria da seção, só existem duas possibilidades para a forma como o fluxo de cisalhamento pode correr sobre a figura.
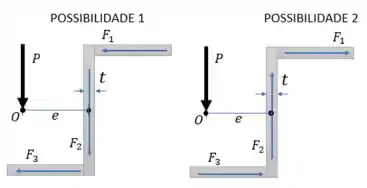
Esta é uma figura estática, então a soma de suas forças tem que ser iguais a zero:
Observe que nas duas possibilidades para o fluxo de cisalhamento as forças e apontam para o mesmo sentido e direção. Então para que isso seja possível:
Passo 2
Como as forças e são iguais a zero, podemos fazer o desenho abaixo:
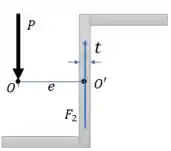
Novamente, a seção é estática, então o somatório de momentos em qualquer ponto é igual a zero. Então se fizermos o somatório de momentos no ponto , por exemplo
Como podemos afirmar que