A viga está sujeita à carga mostrada na figura. Determine a equação da linha elástica. EI é constante.
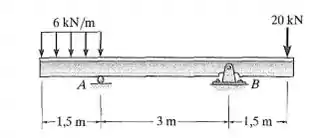
Passo 1
Fala! A gente quer as equações da linha elástica para essa viga. Vamos usar as funções de Macaulay para isso. Aí a gente só precisa achar uma equação.
E para facilitar, vamos usar a tabelinha 12.2 também.
Primeira coisa é calcular s reações de apoio dessa viga fofa:
Considerando que nossas reações estão para cima:
Passo 2
Aí para usar a tabela 12.2, fazemos um esqueminha, colocando com origem na extremidade direita e mostrando a posição de cada força em relação a ele, deixando só a extremidade esquerda de fora. Assim:
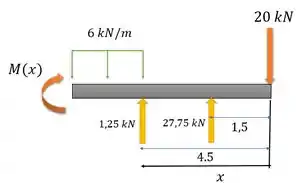
A gente deixou a origem de na direita, para que ao andar para a esquerda, o carregamento distribuído vá até o final da viga. Aí a gente pode usar a tabelinha para ela também.
Aí para montar a equação de fato, olhamos cada força aplicada. A primeira é a de . Ela está distante do ponto onde calculamos , e causa um momento no mesmo sentido, então:
Depois temos a força . Usando a tabelinha, para forças pontuais com sentido para cima, distantes da origem, o momento fica:
Acontece algo parecido para , onde :
E para a força distrubuída que começa distante da origem e vai até o fim da viga, a fórmulinha é:
Passo 3
Montando a equação do momento, ficaremos com:
Sabemos que:
Integrando cada lado 2 vezes, temos:
Passo 4
As condições de contorno são:
Isso porque os apoios não permitem deflexão.
Aqui a gente lembra que as funções são zero se .
Logo, teremos:
Rsolvendo esse sistema:
Logo, a equação será: