25. A treliça é feita de barras de aço e cada uma delas tem seção transversal circular. Se a carga aplicada for , determine, com aproximação de múltiplos de , o diâmetro do elemento estrutural que impedirá que esse elemento estrutural sofra flambagem. As extremidades dos elementos estruturais estão acopladas por pinos.
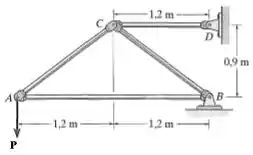
Passo 1
Primeiro, vamos montar o diagrama de corpo livre da estrutura:
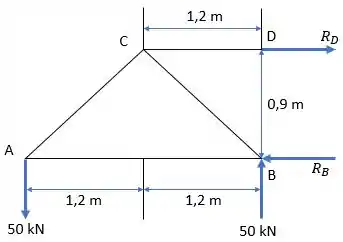
Aqui, devemos fazer o somatório de forças e momentos para encontrar as reações e :
Agora, vamos analisar o ponto :

Mas não sabemos , então como fazemos?
Primeiro, a gente pode ver que a diagonal vale (triângulo ).
Depois, é só a gente fazer a relação entre as medidas do triângulo e a força e suas componentes:
É possível achar de forma semelhante ao jeito de achar , coma diferença de que em vez de , usamos :
Como já achamos :
Passo 2
Fórmula de cálculo da força crítica na flambagem para o ponto :
Como as extremidades estão presas por pinos, temos .
O momento de inércia, como é uma seção circular, é dado pela fórmula:
E temos, também, por ser dado no enunciado que é um aço :
Passo 3
Vamos calcular a tensão devido à força crítica para verificar se ele ultrapassa a tensão de escoamento :
Como , a carga crítica é admissível nessa haste.
Resposta
Achamos, portanto, o valor do diâmetro do elemento que impedirá que a estrutura sofra flambagem, com aproximação de múltiplos de é: