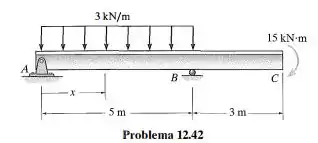
A viga está sujeita à carga mostrada na figura. Determine as equações da inclinação e da linha elástica. EI é constante
Passo 1
Vamos começar calculando as reações de apoio
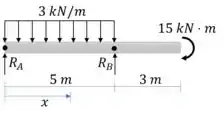
Passo 2
Agora vamos usar as equações de singularidade da tabela 12.2
Porém, tem um leve problema, a carga distribuída não vai até o fim da viga, então será preciso completar a carga por uma equivalente

Vamos então o usar o carregamento equivalente para gerar a equação de momento da viga:
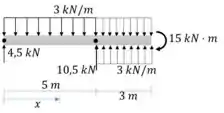
Vamos simplificar a expressão. As singularidades do tipo , se tiver podem ser escritas como :
Passo 3
Agora vamos integrar a equação do momento para obter a equação da inclinação:
A equação da inclinação é:
Passo 4
Agora vamos integrar novamente para determinar a equação da flexão:
A equação da linha elástica é:
Passo 5
Pela condição de contorno no pino A temos:
Aplicando esses valores na equação da linha elástica:
Passo 6
Pela condição de contorno no apoio B:
Aplicando esses valores na equação da linha elástica:
Resposta
Equação da inclinação:
Equação da linha elástica: