Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 6.Problemas - Ex. 21
Represente graficamente os diagramas de força cortante e momento fletor para a viga e determine a força cortante e momento na viga em função de , .
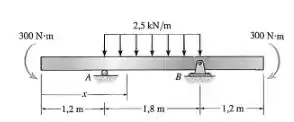
Passo 1
Fala galerinha bonita, tudo beleza?
Primeiramente, devemos calcular as reações de apoio. Para isso, vamos utilizar as equações de equilíbrio:
Logo:
Do mesmo modo para a força:
Tal que:
Passo 2
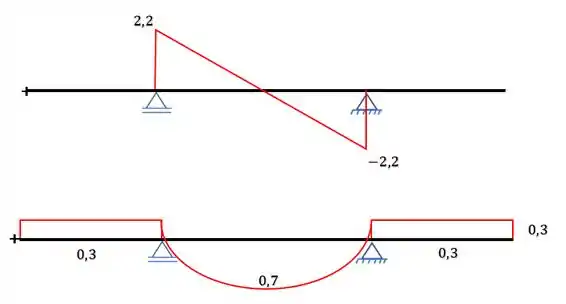
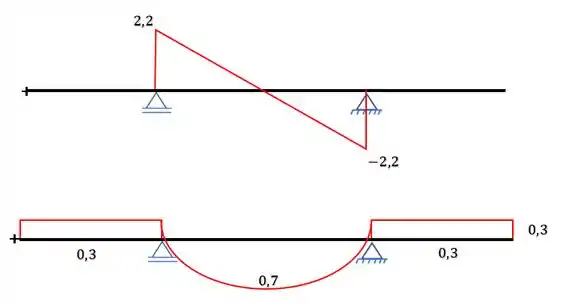
Com as reações, podemos fazer os diagramas de cortante e de momento fletor, respectivamente:
Passo 3
Agora, vamos percorrer a viga e ver como os esforços variam no intervalo pedido. Para o momento, pegamos a força e multiplicamos pela distância:
Para acharmos o cortante, basta derivar a equação do momento:
Resposta
Exercícios de Livros Relacionados
A haste curvada AD de raio r tem peso por comprimento w. Se ela estiver no plano horizontal, determine as cargas internas resultantes que agem na seção transversal que passa pelo ponto B. Dica: A dist
A haste curvada tem raio r e está presa em B. Determine as cargas internas resultantes que agem na seção transversal que passa pelo ponto A, o qual está localizado a um ângulo θ em relação à horizonta
Um elemento diferencial tomado de uma barra curva é mostrado na figura. Mostre que d n d θ = V ; d V d θ = N ; d M d θ =- T e d T d θ = M . dM/dθ
O cano tem massa de 12 kg/m e está preso à parede em A. Determine as cargas internas resultantes que agem na seção transversal que passa por B.
A viga é feita de um poliéster cuja curva tensão-deformação e mostrada na figura. Se a curva puder ser representada pela equação σ = 140 tg-1(15ε) MPa, onde tg-1(15ε) é dada em radianos, determine o v