Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 9.Problemas - Ex. 139
Para a viga e o carregamento mostrados na figura, determine (a) a inclinação na extremidade A, (b) a inclinação na extremidade B e (c) a deflexão no ponto médio C.
Passo 1
Opaa! Fala pessoal, beleza? Bora pra mais um?! Para resolver esse exercício, vamos utilizar o método do momento de área. Para isso vamos precisar desenhar o diagrama M/EI para a viga. Depois disso, sabemos que a área entre dois pontos sob a curva M/EI representa a inclinação entre esses dois pontos. E para obter a deflexão, vamos utilizar o teorema do segundo momento de área, que nos fornece o desvio tangencial entre dois pontos. Sabendo disso, temos tudo o que precisamos para resolver o exercício, então bora lá!
Passo 2
Tá legal, devido a simetria do carregamento, sabemos que as forças nos apoios A e B serão iguais e correspondem a metade da força exercida pelo carregamento distribuído, ou seja:
Agora, também devido a simetria do carregamento, o momento exercido na viga será zero nos apoios e máximo no ponto médio C. Sabemos que teremos duas forças exercendo momento na viga, a força no apoio e o carregamento distribuído. A força no apoio exercerá um momento linear da seguinte forma:
E o carregamento distribuído por sua vez, irá exercer um momento 2 igual a:
Agora vamos calcular os momentos no ponto C da viga, onde teremos:
Passo 3
Agora podemos desenhar o diagrama M/EI para a nossa viga, só lembrando que como temos EI diferente para as seções, isso irá impactar na magnitude do gráfico, pois quanto maior EI, menor será o valor da curva M/EI para um mesmo valor de momento. Então, com os momentos que encontramos, teremos:
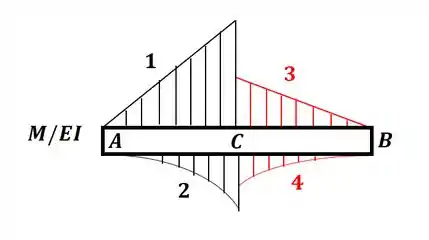
Então, agora vamos calcular as áreas que encontramos e os seus centroides, então vamos lá:
Passo 4
Beleza, agora, sabemos que a inclinação no ponto A pode ser encontrada através da equação 9.22 vista nessa seção, onde teremos:
E, sabemos que o desvio tangencial do apoio B em relação a A é dado por:
Substituindo os valores conhecidos, chegamos em:
Então a inclinação em A será:
Passo 5
Agora, para encontrar a inclinação no ponto B, basta utilizar o teorema do primeiro momento de área, onde teremos:
Isolando a inclinação em B e substituindo os valores conhecidos, teremos:
Estamos quase lá, falta só a C agora.
Passo 6
Beleeeza! Agora, sabemos que a deflexão entre dois pontos será dada através do teorema do segundo momento de área, onde para o nosso caso, teremos:
Em que é a área embaixo da curva e é a distância do centroide da área até o eixo vertical que passa pelo ponto de interesse, que no nosso caso é o ponto C. Então, utilizando as áreas que temos no nosso diagrama , teremos:
Sabendo que não teremos deflexão em A devido ao apoio e substituindo os valores conhecidos, chegamos em:
Tooop! Terminamos mais um!!