Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 6.Problemas - Ex. 105

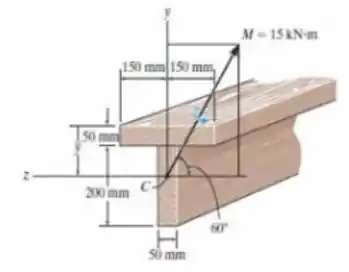
A viga em T está sujeita a um momento fletor M = 15 kN.m direcionado, como mostra a figura. Determine a tensão de flexão máxima na viga e a orientação do eixo neutro. A localização y do centroide, C, deve ser determinada.

Passo 1

Oi oi, meu xuxuzinho!! Tudo bem com você?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora!! Bom, nosso enunciado nos diz que essa viga tem um formato de T e um momento aplicado a 60° do eixo horizontal, e nos pede a tensão de flexão máxima e a orientação do eixo neutro.

A gente vai fazer isso calculando a linha neutra e o momento de inércia, depois é só utilizar a equação da tensão normal em função do momento fletor, então partiu!

Passo 2

Nosso primeiro passo será calcular nossa posição da linha neutra da viga e os momentos nos eixos y e z.

y = ∑ A ⋅ y ∑ A

Aqui a gente vai utilizar os dois componentes do perfil, como é um “T” temos uma barra vertical e outra horizontal:

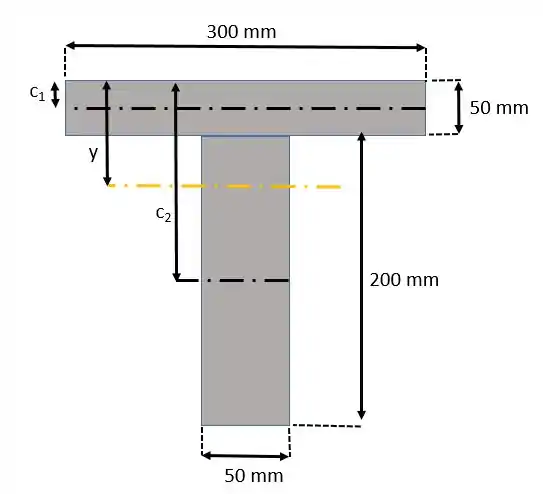
Aqui y representa a altura da linha neutra (laranja), enquanto c 1 e c 2 representam os centroides de cada elemento, valendo, respectivamente, 25 m m e 150   m m . Assim, a linha neutra é calculada como:

y = 50 ⋅   200 150 + ( 50 ⋅ 300 ) ( 25 ) 50   ⋅   200 + ( 50   ⋅ 300 ) = 75   m m

Passo 3

Agora vamos calcular o momento fletor decompondo-o nos eixos z e y :

∑ M = 0

M z =   15 cos ⁡ 60 ° =   7,5   k N . m

M y = 15   s e n 60 ° = 12,99   k N . m

Passo 4

Pronto!! Com os momentos calculados, vamos calcular o momento de inércia. Lembrando que o momento de inércia de uma barra é dado por:

I 0 = b h 3 12

Às vezes precisamos do teorema dos eixos paralelos.

I = I 0 + A ⋅ d 2

Para o cálculo do momento de inércia em y vamos ter o eixo vertical (passando pelo centroide de ambas as barras, então não precisamos fazer o teorema dos eixos paralelos.

I = b 1 h 1 3 12 + b 2 h 2 3 12

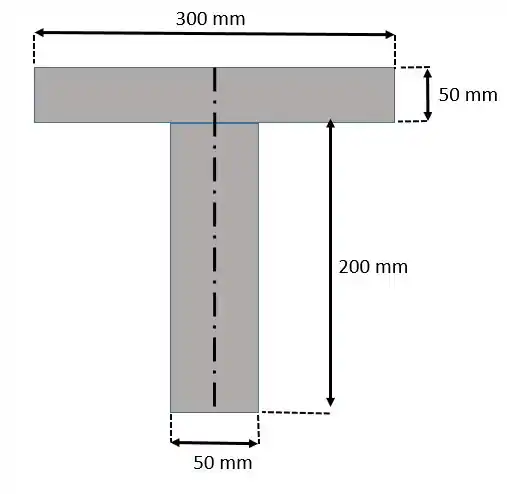
obs: É importante lembrar que o termo que está elevado a 3 sempre é o lado perpendicular ao eixo.

I y =   0,200 ⋅ 0,050 3 12 + 0,050   ⋅   0,300 ³ 12 = 1,1458   x   10 - 4   m

Já para o eixo z vamos precisar aplicar o teorema dos eixos paralelos porque o eixo não coincide com os centroides, por isso é importante achar a distância d da fórmula.

I 0 = b h 3 12

I = I 0 + A ⋅ d 2

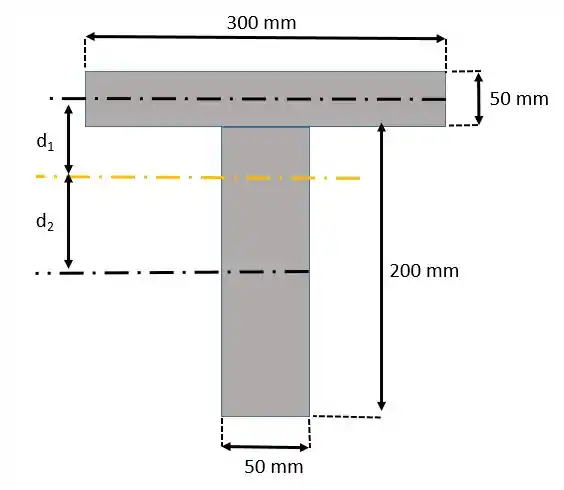
Lembrando que o momento é calculado em torno do eixo da linha neutra representado em laranja na qual y = 75   m m como representado anteriormente.

Para a barra horizontal:

I 0 = 0,3 ⋅   0,05 3 12

A ⋅ d 1 2 = 0,3   ⋅   0,05   ⋅   0,05 2

Logo:

I z 1 = 0,3 ⋅   0,05 3 12 + 0,3   ⋅   0,05   ⋅   0,05 2

Para a barra vertical:

I 0 = 0,05 ⋅   0,2 3 12

A ⋅ d 2 2 = 0,05   ⋅   0,2   ⋅   0,075 2

Logo:

I z 1 = 0,05 ⋅   0,2 3 12 + 0,05   ⋅   0,2   ⋅   0,075 2

Somando-se os dois termos:

I z = 0,05 ⋅   0,2 3 12 + 0,05   ⋅   0,2   ⋅   0,075 2 + 0,3 ⋅   0,05 3 12 + 0,3   ⋅   0,05   ⋅   0,05 2

I z = 1,30208 ⋅   10 - 4 m

Passo 5

Agora que já temos todo o necessário para calcular nossas tensões, por que vamos esperar?? Só bora comigo.

σ m á x = -   M z   y I z +   M y   z I y

σ m á x = -   - 7500 ⋅   0,075 1,30208   ⋅   10 - 4 +   12990 ⋅   0,150 1,1458 ⋅ 10 - 4

σ m á x = 21,9   M P a

Agora para achar a orientação do ângulo neutra vamos fazer utilizar a relação:

I y ⋅ t g   α = I z ⋅ t g θ    

t g   α = I z ⋅ t g θ I y    

t g   α = 1,1458   ⋅   10 - 4 ⋅ t g θ 1,1458   ⋅   10 - 4    

t g   α = t g θ  

  α =   6 3 °

Resposta

σ m á x = 21,9   M P a

α =   6 3 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O momento M é aplicado a uma viga de seção transversal mostrada, em um plano formado um ângulo β com a vertical. Determinar:A tensão no ponto A;A tensão no ponto B;O ângulo que a linha neutra forma co
O momento M é aplicado a uma viga de seção transversal mostrada, em um plano formado um ângulo β com a vertical. Determinar:A tensão no ponto A;A tensão no ponto B;O ângulo que a linha neutra forma co
Duas lâminas de latão são firmemente unidas a um perfil extrudado de alumínio, como mostrado. Usando os dados abaixo, determinar o maior momento fletor permissível, quando o membro composto é curvado
Duas lâminas de latão são firmemente unidas a um perfil extrudado de alumínio, como mostrado. Usando os dados abaixo, determinar o maior momento fletor permissível, quando o membro composto é curvado
O perfilm mostrado é formado pela flexão de uma placa fina de aço. Considerando que a espessura t é pequena quando comparada ao comprimento a dos lados do perfil, determine a tensão (a) no ponto A, (b