Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 5.Problemas - Ex. 63
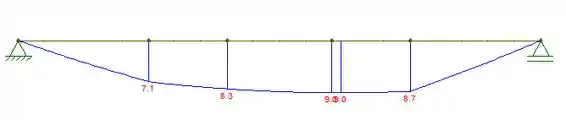
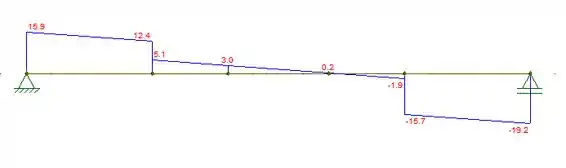
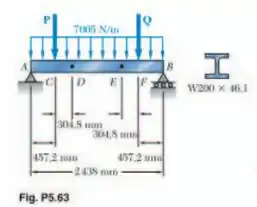
A viga suporta uma força uniformemente distribuída de e duas forças concentradas e A tensão normal provocada pelo momento fletor na borda inferior da viga é de em e de em (a) Trace os diagramas de força cortante e momento fletor para a viga. (b) Determine a tensão normal máxima provocada pelo momento fletor que ocorre na viga.
Passo 1
Fala aí, galerinha. Tudo bem com vocês? Partiu outra questão.
Primeiramente, sabemos que a tensão normal é dada por:
Para este perfil, sabemos que:
Logo, usando as tensões, podemos encontrar o momento nos pontos e
Passo 2
Para determinar as forças, vamos considerar apenas o trecho Sabemos que, no trecho considerado:
Como o somatório de forças deve ser nulo:
Passo 3
Agora, vamos considerar o trecho Aplicando a equação de equilíbrio:
Como o somatório de forças vertical é nulo:
Passo 4
Por fim, vamos considerar o trecho Aplicando a equação de equilíbrio:
Novamente, para equilíbrio de forças verticais:
Passo 5
Com as forças calculadas, basta fazer os diagramas. O diagrama de cortante será:
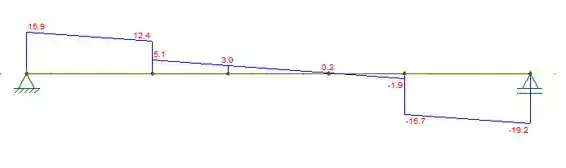
Já o de momento:
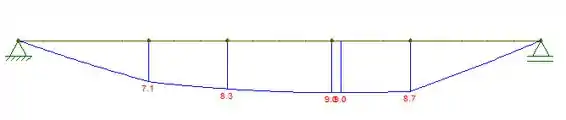
Passo 6
Agora, basta determinar a tensão normal máxima, que será função do momento máximo. Logo:
Substituindo:
Resposta
