Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 12.Problemas - Ex. 110

A viga tem E 1 I 1 constante e é suportada pela parede fixa em B e pela haste AC. Se a haste tiver área de seção transversal A 2   e o material tiver módulo de elasticidade E 2 , determine a força na haste.

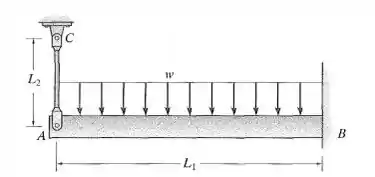
Passo 1

Fala aí pessoal, partiu mais um problema de resmat. Primeiramente, vamos fazer o DCL para entender melhor:

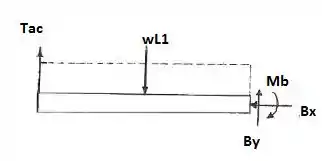
Agora vamos construir a função do momento atuante para podermos usar a equação da linha neutra:

M x = T A C x - w x 2 2

Sabemos que:

E I d v 2 d x 2 = M x

Integrando-se duas vezes as equações do momento, temos:

E 1 I 1 v = T A C x 3 6 - w x 4 24 + C 1 x + C 2

Para a determinação das constantes, temos que aplicar as condições de contorno. As condições de contorno são:

x = L 1 → v = 0  

d v d x = 0

Logo:

C 1 = w L 1 3 6 - T A C L 1 2 2

C 2 = 8 T A C L 1 3 - 3 w L 1 4 24

Passo 2

Agora vamos utilizar um ponto para determinar o deslocamento máximo:

x = 0

V m á x = L 1 3 24 E 1 I 1 8 T A C L 1 3 - 3 w L 1 4

Sabemos que o deslocamento máximo também é dado por:

V m á x = - T A C L 2 A 2 E 2

Igualando-se as duas equações, teremos:

T A c = 3 A 2 E 2 w L 1 4 8 A 2 E 2 L 1 3 + 3 E 1 L 1 L 2

Resposta

T A c = 3 A 2 E 2 w L 1 4 8 A 2 E 2 L 1 3 + 3 E 1 L 1 L 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine as reações ao momento nos apoios A e B. EI é constante.
Determine as reações ao momento nos apoios A e B. Use o método da integração. EI é constante.
Determine a deflexão máxima entre os apoios A e B. EI é constante. Use o método da integração.
Determine as reações nos apoios A e B; em seguida, trace o diagrama de momento fletor. EI é constante.
Para a viga uniforme em balanço e o carregamento mostrados na figura, determine (a) a inclinação e (b) a deflexão no ponto A. Use E = 200 GPa.