Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 9.Problemas - Ex. 77
Para a viga e o carregamento mostrados na figura, determine a inclinação na extremidade e a deflexão no ponto . Use
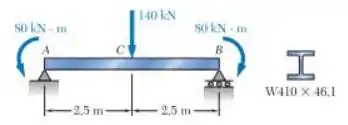
Passo 1
Fala aí, galera. Tudo beleza? Vamos fazer mais uma questão pra tirar aquele notão na prova.
Para determinarmos a inclinação na extremidade . Para isso, vamos utilizar o método da superposição.
Primeiro, temos que esboçar o problema por meio da superposição dos casos de carregamento. São eles, respectivamente, carregamentos , e :
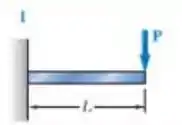
Já o carregamento vai ser:
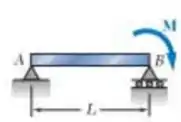
E para o terceiro carregamento:
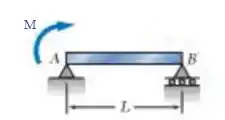
Onde:
Esses carregamentos de superposição correspondem, respectivamente, aos casos , e do apêndice do nosso livro.
Passo 2
Agora que identificamos os casos de carregamentos para a superposição, vamos utilizar as equações que a gente encontra no mesmo apêndice para determinarmos a deflexão e inclinação para cada caso.
Para o carregamento , temos que a deflexão no ponto é dada pela equação da linha elástica para este tipo de carregamento em . Fica assim:
E para a inclinação no ponto , em :
Substituindo:
Agora que encontramos a deflexão e a inclinação para o primeiro carregamento, bora fazer o mesmo para o segundo.
Para o caso do nosso livro, temos que a inclinação na extremidade vai ser:
Substituindo:
Podemos encontrar a deflexão no ponto a partir da equação da linha elástica. Para este caso, ela é tabelada e dada por:
Por fim, para o carregamento , temos novamente o caso de carregamento. Portanto, a inclinação no ponto vai ser:
Substituindo:
Já a deflexão no ponto vai ser:
Passo 3
Então, agora que encontramos a deflexão e a inclinação para cada caso de superposição, vamos determinar a inclinação no ponto . Ela é dada pela soma das inclinações dos três casos de superposição. Portanto:
Para a seção , o momento de inércia é tabelado. Seu valor é:
Substituindo:
E para encontramos a deflexão no ponto , temos novamente um somatório, só que desta vez, é das deflexões nos casos. Portanto:
Substituindo :
Isso é tudo, pessoal! Bora zerar esse livro.