Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 7.Problemas - Ex. 119

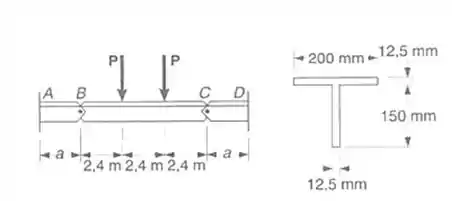
As vigas AB, BC e BD tem seções transversais como mostrado e são articuladas por pinos conectores em B e C. Sabendo-se que σ adm= 150 MPa na tração e σadm= -110 MPa na compressão, determinar a) o maior valor admissível de P para que a viga BC não sejam ultrapassada as tensões admissíveis b) máxima distancia “a” para que a viga em balanço AB e CD as tensões admissíveis também não sejam excedidas.

Passo 1

E ai gurizada tudo belezinha??? Partiu calcular valor admissível de P para que a viga BC não sejam ultrapassada as tensões admissíveis?? Vem comigooo!!

Para isso vamos considerar então que:

M b = M c = 0

V b = - V c = P

Vamos esquematizar agora gurizada para podermos encontrar o momento em e (Me):

∑ M e = F × d

∑ M e = 0 + 2,4 × P = 2,4 P

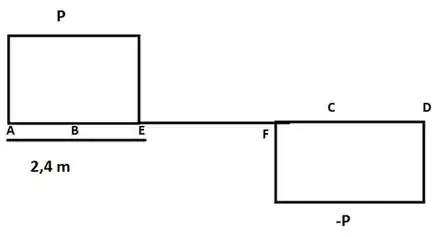
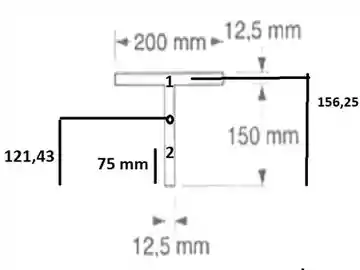
Gurizada agora que fizemos as equivalências temos que encontrar o momento de inercia deste perfil dado no enunciado (perfil T), para isso temos que encontrar a centroide, vamos cotar o perfil dado como abaixo, observem. A região foi dividia em 1 e 2 (tração e compressão).

Agora gurizada vamos montar uma tabelinha para calcularmos a área, inércia e afins, conforme as dimensões do perfil acima.

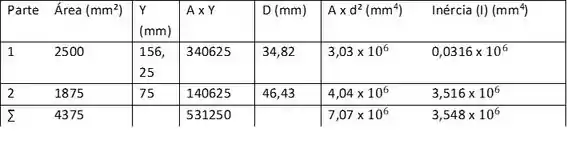
Gurizada agora precisamos relacionar a inércia no topo e na base do perfil, pois como vocês podem analisar, não é simétrico como um perfil “I” por isso devemos distingui-los ...

Antes devemos encontrar “Y” (centroide) veja só:

Y = A Y / A

Y = 531250 4375 = 121,43   m m

Agora que encontramos o centroide do perfil inteiro vamos encontrar a inércia, vem comigo!!

I = ∑ A d 2 + ∑ I = 7,07   x   10 6 + 3,548   x   10 6 = 10,621 x   10 6 m m 4

Galeraaaa agora que temos a inércia podemos achar os momentos em ambas regiões

Lembrando que o momento para este caso é calculado como:

M =   - σ I Y

T r a ç ã o   E F =   - 110 x   10 6 × 10,621 x 10 6 121,43 = 9,62 x 10 3 N m

Gurizada para os demais cálculos é o mesmo esquema...

C o m p r e s s ã o   E F = 150 x   10 6 × 258,6   x   10 6 = 38,9   x 10 3 N m

T r a ç ã o   A D = - 110 x   10 6 × 258,6   x   10 6 = - 28,45   x   10 3 N m

C o m p r e s s ã o   A D = 150 x   10 6 × - 37,47   x   10 6 = - 13,121   x   10 3 N m

Agora simmm gurizada podemos encontrar o P, vem comigo :D

M e = 2,4 P

P = 4 ,   01   K N

Passo 2

b) Agora vem comigo para encontrarmos máxima distancia

Se considerarmos que:

V A =   P

A área do diagrama de A a B chamaremos de “a”

a V A =   a P

Então fazendo o momento em A temos:

M A = - a P = - 4,01 x   10 3 a = - 13,121   x   10 3

a = 3,27   m

Ufaaaa acabou 0/

Resposta

a ) 4 ,   01   K N

b ) a = 3,27   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A junta está presa por dois parafusos. Determine o diâmetro exigido para os parafusos se a tensão de ruptura por cisalhamento para os parafusos for τ r u p=350M P a . Use um fator de segurança para ci
O tamanho a do cordão de solda é determinado pelo cálculo da tensão de cisalhamento média ao longo do plano sombreado, que tem a menor seção transversal. Determine o menor tamanho a das duas soldas se
O elemento B está sujeito a uma força de compressão de 4k N . Se A eB forem feitos de madeira e tiverem 10m m de espessura, determine, com aproximação de 5m m , a menor dimensão h do apoio de modo que
O tamanho do cordão de solda é a=8m m . Considerando que a junta falhe por cisalhamento em ambos os lados do bloco ao longo do plano sombreado, que é a menor seção transversal, determine a maior força
O método do Coeficiente de Projeto para Carga e Resistência deve ser utilizado para selecionar os dois cabos a serem utilizados para subir e descer uma plataforma com dois operários lavadores de janel