Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 1.Problemas - Ex. 80
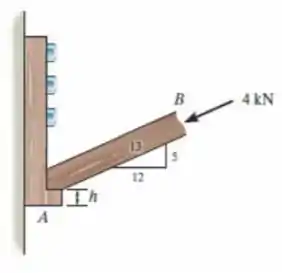
O elemento está sujeito a uma força de compressão de . Se e forem feitos de madeira e tiverem de espessura, determine, com aproximação de , a menor dimensão do apoio de modo que a tensão de cisalhamento média não exceda .
Passo 1
Queremos encontrar o valor mínimo para de tal forma que a nossa tensão de cisalhamento média não exceda o valor dado no enunciado. Lembrando que a força que vai causar o cisalhamento vai ser a força vertical de B que chamaremos aqui de .
Passo 2
A força em B pode ser decomposta em duas componentes que aqui nos interessa a componente vertical que podemos definir como
Assim, podemos definir o nosso a partir da tensão média dada por
Aproximando em até 5mm vamos obter
Resposta
Exercícios de Livros Relacionados
Determine as menores dimensões do eixo circular e da tampa circular se a carga que devem suportar é P=150k N . A tensão de tração, a tensão de apoio e a tensão de cisalhamento admissíveis são σ t a d
A estrutura está sujeita ao carregamento distribuído de 2k N / m . Determine o diâmetro exigido para os pinos em A e B se a tensão de cisalhamento admissível para o material for τ a d m =100M P a . Am
Se a tensão de apoio admissível para o material sob os apoios em A e B for σ aa d m =2,8M P a , determine os tamanhos das chapas de apoio quadradas A 'eB ' exigidos para suportar a carga. Considere P=
Se a tensão de apoio admissível para o material sob os apoios em A e B for σ aa d m =2,8M P a , determine a carga P máxima que pode ser aplicada à viga. As seções transversais quadradas das chapas de
A lança é suportada pelo cabo do guincho com diâmetro de 6m m com tensão normal admissível σ a d m = 168 M P a . Se a lança tiver de levantar lentamente uma carga de 25 k N , de θ = 20 ° até θ = 50 °