Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 1.Problemas - Ex. 84
O tamanho do cordão de solda é determinado pelo cálculo da tensão de cisalhamento média ao longo do plano sombreado, que tem a menor seção transversal. Determine o menor tamanho das duas soldas se a força aplicada à chapa for . A tensão de cisalhamento admissível para o material da solda é .
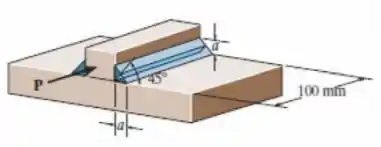
Passo 1
Primeiramente devemos observar que a área sombreada a qual o problema fala está angulada de , então, a área que vamos usar é, na verdade
Como o problema nos deu a tensão de cisalhamento admissível, então, vamos utilizá-la para determinar a dimensão de , logo devemos lembrar que a tensão de cisalhamento média é dada por
Passo 2
No nosso caso a nossa força vai ser a metade do valor de haja vista que ocorre um cisalhamento duplo, assim
Resposta
Exercícios de Livros Relacionados
Os dois cabos de aço A B e A C são usados para suportar a carga. Se ambos tiverem uma tensão de tração admissível σ a d m = 200 M P a , determine o diâmetro exigido para cada cabo se a carga aplicar f
A manivela está presa ao eixo A por uma chaveta d e de 25m m . Se eixo for fixo e uma força vertical de 200N for aplicada perpendicularmente ao cabo, determine a dimensão d se a tensão de cisalhamento
O parafuso de olhal é usado para sustentar a carga de 25k N . Determine seu diâmetro d com aproximação de múltiplos d e5m m e a espessura exigida h com aproximação de múltiplos de 5m m do suporte de m
A estrutura está sujeita a carga de 8k N . Determine o diâmetro exigido para os pinos em A e B se a tensão de cisalhamento admissível para o material for τ a d m =42M P a . O pino A está sujeito a cis
As hastes A B e C D são feitas de aço cuja tensão de ruptura por tração é σ r u p=510M P a . Usando um fator de segurança F S=1,75 para tração, determine o menor diâmetro das hastes de modo que elas p