Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.3 - Ex. 45

O volante gira no sentido horário com uma velocidade constante de 600   r p m . A haste de conexão A B desliza através do cursor articulado em C . Calcule a velocidade angular ω de A B para o instante em que θ = 60 ° .

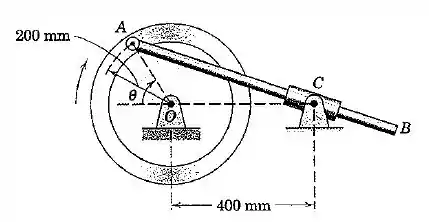
Passo 1

Vamos começar dando nome a um ângulo muito importante para o problema:

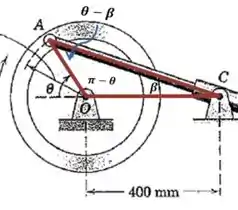
E nosso objetivo é justamente calcular a derivada temporal de β . Precisamos achar alguma relação geométrica que envolva esse ângulo, e então derivar em relação ao tempo.

Sabemos que o raio do círculo é 0,2   m , então pela lei dos senos podemos escrever o seguinte:

0,2 sen ⁡ ( β ) = 0,4 sen ⁡ ( θ - β )

sen ⁡ ( θ - β ) = 2 sen ⁡ ( β )

E podemos derivar essa equação em relação ao tempo:

θ ˙ - β ˙ cos ⁡ ( θ - β ) = 2 β ˙ cos ⁡ ( β )

Agora vamos isolar β ˙ :

θ ˙ cos ⁡ ( θ - β ) = β ˙   2 cos ⁡ β + cos ⁡ θ - β

β ˙ = cos ⁡ θ - β 2 cos ⁡ β + cos ⁡ θ - β   θ ˙

Passo 2

Agora queremos achar o valor de β ˙ no caso em que θ = 60 ° . Já temos o valor de θ ˙ :

θ ˙ = 600   r p m = 600 r o t m i n   1 60 m i n s e g   2 π r a d r o t ≅ 62,8   r a d / s

Falta apenas encontrar o valor de β nesse instante, e teremos todas as variáveis necessárias. Podemos construir um triângulo retângulo para achar esse valor:

tan ⁡ β = 0,2 sen ⁡ θ 0,4 + 0,2 cos ⁡ θ

Como θ = 60 ° , temos:

tan ⁡ β = 0,3464         ⇒           β = 19,11 °

Passo 3

E agora podemos substituir tudo na nossa fórmula para encontrar β ˙ :

β ˙ = cos ⁡ 60 ° - 19,11 ° 2 cos ⁡ 19,11 ° + cos ⁡ 60 ° - 19,11 ° ( 62,8 )

β ˙ = ω = 17,94   r a d / s

Resposta

A velocidade angular é ω = 17,94   r a d / s .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

5/58) Um dos mecanismos mais comuns é o de cursor e manivela . Expresse a velocidade angular ω A B e a aceleração angular α A B da biela A B em termos do ângulo da manivela θ para uma determinada velo
5/48) O cilindro hidráulico C fornece à extremidade A da barra A B uma velocidade constante v 0 no sentido negativo de x . Determine expressões para a velocidade angular ω = θ ' e aceleração angular α
5/52) As duas engrenagens formam uma unidade integrada e giram sobre a cremalheira fixa . A engrenagem maior tem 48 dentes , e a rosca sem fim gira com uma velocidade de 120r p m . Determine a velocid
5/49) Deseja-se projetar um sistema para controlar a taxa de extensão x ' da escada de um caminhão de incêndio durante a elevação da escada de modo que o cesto B tenha apenas um movimento vertical . D