Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.3 - Ex. 48

5/48) O cilindro hidráulico C fornece à extremidade A da barra A B uma velocidade constante v 0 no sentido negativo de x . Determine expressões para a velocidade angular ω = θ ' e aceleração angular α = θ " da barra em termos de x .

Passo 1

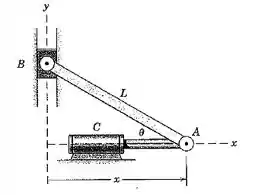
Então pessoal , analisando o triângulo fornecido pelo enunciado , temos que :

x = L cos ⁡ θ

Agora derivaremos dos dois lados para acharmos uma relação que nos forneça a velocidade angular :

x ' = - v 0 = - L   θ ' sen ⁡ θ

Logo ,

ω = θ ' = v 0 L sen ⁡ θ

Onde , novamente pela análise do triângulo , observamos que :

L sen ⁡ θ = y = L 2 - x 2

Então ,

ω = v 0 L 2 - x 2

Passo 2

Bom galera , agora que sabemos a velocidade angular , tudo fica mais fácil . Sabemos que :

α = θ " = ω '

Portanto , derivando a equação obtida no passo anterior , achamos que :

α = θ " = v 0 L d d t csc ⁡ θ = v 0 L   ( - c t n θ csc ⁡ θ ) θ '  

Logo ,

α = - v 0 L x y L y   θ '

Substituindo o valor de θ ' achado no passo anterior , por sua vez , achamos que :

α = - x v 0 2 y 2 L 2 - x 2

Logo ,

α = - x v 0 2 L 2 - x 2 3 2

Resposta

ω = v 0 L 2 - x 2

α = - x v 0 2 L 2 - x 2 3 2

Suave galera? Então bora pra próxima!!!

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A lança O A está sendo elevada pelo arranjo de cabo e polia mostrado. Se o ponto B no cabo recebe uma velocidade constante v B = 3,2m / s , determine a velocidade angular ω e a aceleração angular ∝ da
O movimento do volante enquanto rola para cima a cremalheira fixa sobre o seu núcleo dentado é controlado por meio do cabo periférico pela roda motora D , que gira no sentido anti-horário na taxa cons
O movimento vertical da plataforma de trabalho é controlado pelo movimento horizontal do pino A . Se A possui uma velocidade v 0 para a esquerda, determine a velocidade vertical v da plataforma para q
Calcule a velocidade angular ω da barra esbelta A B como uma função da distância x e da velocidade angular constante ω 0 do tambor.
Um quebra-molas está sendo instalado em uma estrada horizontal para lembrar aos motoristas do limite da velocidade existente. Se o motorista do carro sente em G uma aceleração vertical da mesma ordem