Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.3 - Ex. 57

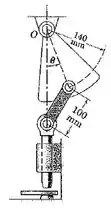
5/57) O punção é acionado por uma oscilação harmônica simples do setor articulado dada por θ = θ 0 sen ⁡ 2 π t   , onde a amplitude é θ 0 = π 12   r a d   ( 15 ° ) e o tempo para uma oscilação completa é de 1 segundo . Determine a aceleração do punção quando (a) θ = 0 e (b) θ = π / 12

Passo 1

Então galera , pelo que foi dado pelo enunciado , temos que :

θ = θ 0 sen ⁡ 2 π t

Derivando para obtermos uma relação com a velocidade angular , achamos que :

θ ' = 2 π θ 0 cos ⁡ 2 π t

Utilizando o mesmo raciocínio do procedimento anterior , derivamos a nova equação obtida para acharmos uma relação com a aceleração angular :

θ " = - 4 π 2 θ 0 sen ⁡ 2 π t ⁡

Além disso , nos é fornecido que :

θ 0 = π 12  

Sendo assim , quando θ = 0 , t = 1 2   s e θ ' = 2 π θ 0 = π 2 6   r a d / s , temos que :

θ " = 0

Da mesma forma , quando θ = π 12 , t = 1 4 s , θ ' = 0 , temos que :

θ " = - 4 π 2 θ 0 = - π 3 3   r a d / s 2  

Passo 2

Bom galera, aplicando a lei dos cossenos ao triângulo indicado pelo enunciado , temos que:

l 2 = y 2 + b 2 - 2 y b cos ⁡ θ  

Ou seja ,

0 - y y ' + y b θ ' sen ⁡ θ - y ' b cos ⁡ θ

Com isso , temos que :

0 = y y " + y '2 + y'b θ ' sen ⁡ θ + yb θ " sen ⁡ θ + y b θ ' 2 cos ⁡ θ - y " b   c o s θ + y ' b θ ' sen ⁡ θ ⁡

y " ( b  cosθ -y)= y '2 +2y'bθ' sen ⁡ θ + ybθ sen ⁡ θ + y b θ ' 2 cos ⁡ θ  

Sendo assim , para θ = 0   , y ' = 0     e   θ " = 0 , temos que :

    y " ( b - [ b + l ] ) = 0 + 0 + 0 + ( b + l ) b π 2 6 2

y " = π 4 36 b b + l - l = - π 4 36 0,14 0,24 0,1 = - 0,909   m / s 2   (   p a r a   c i m a   )

Passo 3

Para θ = π 12   , por sua vez , aplicando a lei dos senos temos que :

  b sen ⁡ β = l sen ⁡ 1 2      

Logo ,

  β = sen - 1 ⁡ 0,14 0,1 sen ⁡ π 12 = 21,24 °

Sendo assim , para y ' = 0       e   θ ' = 0   , temos que :

  y = b cos ⁡ θ + l cos ⁡ β = 0,14 cos ⁡ π 12 + 0,1 cos ⁡ 21,24 ° = 0,2284   m  

y " ( 0,14 cos ⁡ π 12 ⁡ - 0,2284 ) = 0 + 0 + 0,2284 ( 0,14 ) ( - π 3 3 )   sen ⁡ π 12   + 0

y " (-0,09320)=-0,08555 

y" = - 0,918   m / s 2 (   p a r a   b a i x o   )

Resposta

y " = - 0,909   m / s 2   (   p a r a   c i m a   )

y" = - 0,918   m / s 2 (   p a r a   b a i x o   )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Resolva o Problema 16.30, considerando que velocidade angular inicial do volante é de 360 rpm no sentido horário.PROBLEMA 16.30 O tambor de freio de 200 mm de raio é unido a um volante maior que não e
Um disco de raio 180 mm está em repouso quando é colocado em contato com uma correia em movimento com velocidade constante. Desprezando o peso da haste de conexão AB e sabendo que o coeficiente de atr
Para poder determinar o momento de inércia de massa de um volante de raio de 600 mm, um bloco de 12 kg é ligado a um fio que é enrolado em torno do volante de motor. O bloco é solto e observa-se que e
Um tambor de freio de 150 mm é ligado a um volante de motor maior que não é mostrado na figura. O momento de inércia total da massa do tambor e do volante é 75 kg ∙ m2. Uma cinta de freio é utilizada
Dois discos uniformes e dois cilindros são montados como indicado na figura. O disco A tem a massa de 10 kg e o disco B tem a massa de 8 kg. Sabendo que o sistema é liberado do repouso, determine a ac