Critérios de Falha
Teoria
Introdução
Nos últimos tópicos, vimos como analisar as tensões em um ponto para descobrirmos:
- As tensões normais extremas nesse ponto, chamadas de tensões principais;
- E a tensão de cisalhamento máxima nele.
Além disso, em algum momento anterior do curso...
Vimos como os materiais falham quando as tensões neles superam seus limites de resistência, como, por exemplo:
- O Limite de Resistência ao Escoamento de um material, após o qual um material se deforma irreversivelmente;
- E o Limite de Resistência à Tração , após o qual o material quebra.
Agora...
Vamos dizer que nós descobrimos as tensões principais em um certo ponto :
...e que a gente sabe que o material desse ponto falha por escoamento quando as tensões nele atingem o limite .
Nesse caso, como que a gente sabe se o material vai falhar ou não?
Critério da Tensão Normal Máxima
O nosso primeiro instinto pode ser verificar se as tensões normais no ponto superam ou não o limite .
Fazendo isso para o nosso exemplo, veríamos que a maior intensidade de tensão normal no ponto é , o que é bem menor que o limite .
Assim, concluíriamos que o ponto não falha.
Mas a verdade é que esse critério de falha só funciona para materiais frágeis, como o vidro e o acrílico, que falham por quebra/ruptura.
Além disso, esse critério deve usar como seu limite, e não , uma vez que é o limite que caracteriza a falha por quebra/ruptura dos materiais frágeis.
No nosso caso, temos um material dúctil, que falha por escoamento (deformação irreversível), como é o caso do aço, do alumínio e de muitos plásticos.
Então esse critério de falha não vai adiantar para a gente.
Mas como assim???
Por que não???
Critério da Tensão Cisalhante Máxima (Critério de Tresca)
Porque os experimentos mostram que os materiais dúcteis falham devido à tensão de cisalhamento , e não devido à tensão normal .
Daí que, para a tensão cisalhante , o limite de resistência ao escoamento vai ser:
E aí para saber se um ponto vai falhar ou não, devemos verificar se a tensão cisalhante máxima é maior ou menor que .
E como a gente calcula essa tensão ?
Então...
Quando estudamos o estado plano de tensões, vimos que podíamos calcular a tensão cisalhante máxima no plano fazendo que:
Mas calma...
Essa é só a tensão cisalhante máxima no plano.
A verdade é que a tensão cisalhante máxima no ponto precisa levar em conta o fato de que o ponto é um elemento em um espaço 3D.
Por causa disso, existem na verdade 3 “planos principais” que passam em um ponto.
Daí que, em um desses planos, é possível que a tensão cisalhante máxima seja maior que a calculada pela fórmula acima.
Tá... Mas chega de viagem...
Como é então o jeito certo de calcular a tensão cisalhante máxima no ponto?
Usando a fórmula abaixo:
Onde e devem ser a tensão principal máxima e a tensão principal mínima no ponto.
Sendo que (atenção!): Quando estivermos trabalhando com tensões no plano, devemos ter em mente que:
- Além das duas tensões principais e encontradas no plano,
- Irá existir no eixo fora do plano uma terceira tensão principal igual à .
Como mostra o exemplo abaixo:
Voltando para o nosso critério de falha...
Aplicando para o nosso ponto , vamos encontrar que a tensão cisalhante máxima nesse ponto é .
Como isso é maior que , isso significa que o material falharia por esse critério.
Mas calma...
Nem tudo está perdido.
Isso porque esse critério de falha da tensão cisalhante máxima (também chamado de critério de Tresca) é um critério mais conservador.
Existe um terceiro critério que tenta descrever melhor o que realmente acontece com os materiais dúcteis, que é o:
Critério da Máxima Energia de Distorção (Critério de von Mises)
Nesse critério, não é utilizado nem a tensão normal máxima nem a tensão cisalhante máxima.
Ao invés disso, definimos uma nova tensão que de uma certa forma leva em conta todos esses fatores.
Essa nova tensão é chamada de tensão de von Mises , ou e é calculada a partir das tensões principais e usando a fórmula:
Aí, podemos dizer que o material deve falhar se essa tensão de von Mises superar a tensão de escoamento .
Calculando para o nosso exemplo, encontraríamos .
E isso é menor que , o que significa que o material não falharia.
Fatores de Segurança
Para cada um desses critérios, é possível determinar um fator (ou “coeficiente”) de segurança .
O fator de segurança indica quantas vezes o material é mais resistente do que ele precisa ser e é definido como:
De tal forma que:
- Se , a tensão no material vai ser menor ou igual à tensão de falha e o material não vai falhar.
- Mas se , a tensão no material vai superar a tensão de falha e o material vai falhar.
Daí que...
Para o Critério da Tensão Normal Máxima, a tensão de falha vai ser e a tensão no material a tensão normal máxima no ponto, de tal forma que:
Já para o Critério da Tensão Cisalhante Máxima (Critério de Tresca), a tensão de falha é e a tensão no material , então:
Enquanto que para o Critério de von Mises, a tensão de falha é e a tensão no material , de tal forma que:
Dois Comentários Finais
1. Visualização Gráfica
Todos esses critérios de falha podem ser visualizados em um gráfico .
Mas como assim?
Então...
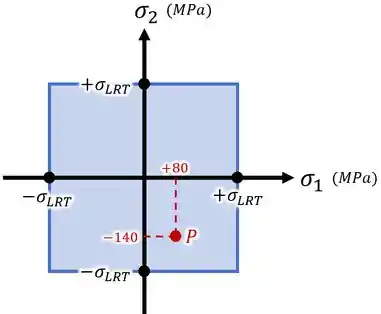
Se a gente usar os pontos em um gráfico para formar um quadrado, esse quadrado vai representar o critério da tensão normal máxima:
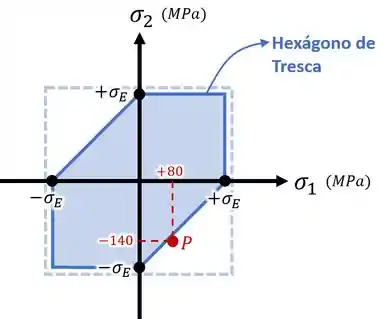
Já formando um hexágono entre os pontos (!) como na imagem abaixo, o hexágono vai representar o critério de Tresca:
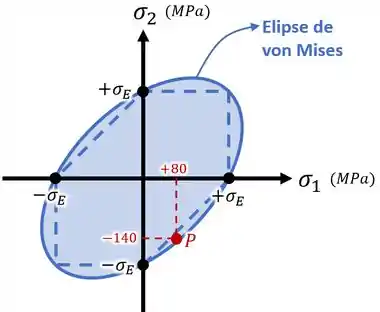
E formando uma elipse inclinada entre esses mesmos pontos , essa elipse vai representar o critério de von Mises:
Daí que...
Inserindo nesses gráficos as tensões principais e do nosso ponto , como foi feito nas imagens acima, vamos ver de acordo com quais critérios o ponto falha ou deixa de falhar.
Se o ponto estiver dentro do quadrado, do hexágono ou da elipse, é porque ele não vai falhar.
E se o ponto estiver fora da região de um certo critério, é porque ele vai falhar de acordo com aquele critério.
2. Tensão de von Mises no Estado Triaxial ou “3D” de Tensões
No caso de estarmos trabalhando com um estado “3D” de tensões, a tensão de von Mises vai ser dada pela fórmula:
Sendo que se a gente pegar essa fórmula acima e fizer , vamos acabar encontrando a fórmula para que vimos anteriormente para o estado plano de tensões:
Critério da Tensão Normal Máxima
Critério da Tensão Cisalhante Máxima (Critério de Tresca)
Critério da Máxima Energia de Distorção (Critério de von Mises)
Fatores de Segurança
Dois Comentários Finais
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração Própria
No estado plano de tensões de um ponto , as tensões principais são e .
Determine, usando os critérios de Tresca e de von Mises, o coeficiente de segurança para esse ponto sabendo que ele é feito de um material que possui um limite de resistência ao escoamento .
Ao final, esboce o hexágono de Tresca e a elipse de von Mises para esse material e mostre a localização do ponto nesses gráficos.
Passo 1
O que está acontecendo?
O exercício nos forneceu as tensões principais em um ponto :
Sendo que, lembra aí, a partir dessas tensões principais máximas e mínimas em um ponto, é possível determinar a tensão cisalhante máxima nesse ponto:
Onde e são as tensões principais máxima e mínima nesse ponto.
Além disso, o exercício ainda nos fornece o limite de resistência ao escoamento desse material.
Sendo que, lembra aí, a partir desse limite , é possível encontrar o limite de resistência ao escoamento por cisalhamento, :
E o que é que o exercício quer?
Ele quer que a gente determine os coeficientes/fatores de segurança para esse ponto usando os critérios de Tresca e de von Mises.
Para tanto, devemos usar as fórmulas:
Lembrando que é o que chamamos de tensão de von Mises, que é definida para um estado plano de tensões como:
Ao final, o exercício ainda quer que a gente esboce o hexágono de Tresca e a elipse de von Mises:
...e mostre a localização do ponto nesse gráfico.
Passo 2
Então vamos lá!
Primeiro, para calcular o fator de segurança de acordo com o critério de Tresca, precisamos calcular:
- O limite de resistência ao escoamento por cisalhamento, :
- E a tensão de cisalhamento máxima no ponto:
Para esse ponto, nós vamos ter as tensões principais no plano , e uma tensão principal no eixo fora do plano de .
Sendo assim, a tensão principal máxima no ponto vai ser e a mínima , de tal forma que:
Feito isso, podemos agora fazer que:
O que vai dar:
O que significa que, pelo critério de Tresca, o material possui vezes a resistência que ele necessita ter.
Passo 3
Agora, para calcular o fator de segurança de acordo com o critério de von Mises, precisamos calcular a tensão de von Mises:
Substituindo e , isso fica assim:
Simplificando os sinais, temos:
E calculando tudo, encontramos que:
Feito isso, podemos agora aplicar:
Substituindo e , encontramos que:
O que dá:
O que significa que, pelo critério de von Mises, o material possui vezes a resistência que ele precisa ter.
Passo 4
Por fim, para completar o exercício, só falta desenharmos o hexágono de Tresca e a elipse de von Mises, usando para tanto que :
Aí, marcando as tensões principais e do ponto nesse gráfico, confirmamos como o ponto não falha de acordo com nenhum critério:
E assim terminamos nosso exercício!
Resposta
Exercício Resolvido #2
Ferdinand P. Beer et al., Mecânica dos materiais, 5ª ed. Porto Alegre: AMGH, 2011, pp. 479-7.81. (Adaptada)
O estado plano de tensão indicado ocorre em um componente de máquina feito de um aço com . Usando os critérios da tensão de cisalhamento máxima (critério de Tresca) e da energia de distorção máxima (critério de Von-Mises), determine se ocorre o escoamento quando:
;
& .
Caso o escoamento não ocorra, determine o coeficiente de segurança correspondente.
Passo 1
O que está acontecendo?
O exercício nos forneceu um estado plano de tensões para um ponto em que:
Sendo que esse ponto é feito de um aço com um limite de resistência ao escoamento .
E o que é que o exercício quer?
Ele quer que a gente determine os coeficientes/fatores de segurança desse ponto acordo com os critérios de Tresca e de von Mises para as situações em que:
;
& .
Sendo que, caso um desses fatores de segurança seja menor do que 1, isso vai significar que vai ter ocorrido o escoamento do material.
Então, para resolver o exercício...
Devemos primeiro calcular as tensões principais nesse ponto em função de .
Feito isso, vamos poder calcular os fatores de segurança para cada valor de de acordo com os critérios de Tresca e de von Mises usando as fórmulas:
Sendo que é importante lembrar que:
E que, para um estado plano de tensões:
Passo 2
Então vamos lá!
Antes de tudo, precisamos determinar as tensões principais no nosso ponto em função de , então vamos fazer isso.
Lembra aí!
Para determinar as tensões principais no estado plano de tensões, podemos:
1. Calcular a tensão normal média no ponto:
Aí aqui, substituindo que , vamos encontrar que:
& 2. Calcular o raio para esse estado de tensões:
Aí, aqui, como , isso vai ficar assim:
O que significa que:
E como , isso significa que:
Feito isso, podemos agora calcular as nossas tensões principais aplicando que:
Aí, substituindo e , vamos encontrar que:
Passo 3
Definidas as tensões principais, podemos agora resolver o item .
Nesse item, temos que , de tal forma que:
Agora, além dessas duas tensões principais no plano, ainda vai haver no ponto uma terceira tensão principal no eixo fora do plano de .
Dessa forma, as tensões principais máxima e mínima para esse ponto são:
Passo 4
Em seguida, para calcularmos o coeficiente/fator de segurança de Tresca, precisamos calcular os termos:
O que, substituindo vai dar:
Aí, usando esses valores para calcular o coeficiente/fator de segurança de Tresca, encontramos que:
O que dá:
Passo 5
Para finalizar o item , devemos calcular o coeficiente/fator de segurança de von Mises.
Para tanto, devemos antes calcular a tensão de von Mises :
Substituindo e e simplificando os sinais, obtemos que:
O que vai dar:
Aí, usando esse valor e para calcular o coeficiente/fator de segurança de von Mises, temos:
O que dá:
Passo 6
Terminado o item , podemos seguir para o item .
Nesse item, temos que , de tal forma que:
Agora (mais uma vez!), além dessas duas tensões principais acima no plano, ainda vai haver no ponto uma terceira tensão principal no eixo fora do plano de .
Dessa forma, as tensões principais máxima e mínima para o ponto são:
Passo 7
Agora, com o objetivo de calcular o coeficiente de segurança de Tresca, precisamos calcular antes a tensão de cisalhamento máxima nesse ponto do item :
Aí, usando esse valor e o valor já calculado lá no passo 4, podemos calcular o coeficiente de segurança de Tresca:
Obtendo assim que:
Sendo que, como esse valor está abaixo de , ele significa que o material do ponto vai escoar/falhar pelo critério de Tresca.
Passo 8
E finalmente, para terminar o exercício, vamos calcular o coeficiente de segurança de von Mises para o item , começando pelo cálculo da tensão de von Mises para esse item:
Substituindo e e simplificando os sinais, obtemos que:
O que dá:
Aí, usando esse valor e para calcular o coeficiente/fator de segurança de von Mises, temos:
E pronto!
Terminamos o exercício.
Resposta
Pelos critérios de Tresca e Von-Mises, temos coeficientes de segurança e , respectivamente.
Pelo critério de Tresca, ocorre o escoamento do material. Já pelo critério de Von-Mises, temos um coeficiente de segurança .
Exercício Resolvido #3
Elaboração própria
Dado o elemento abaixo, determine o fator de segurança pelo método de Tresca e de Von Mises sabendo que a resistência desse material é de
Passo 1
Sabemos que tanto o critério de Tresca, quanto o critério de Von mises dependem das tensões principais que agem nesse elemento, sendo em um necessário a tensão cisalhante máxima, e no outro, sendo necessário a tensão principal maior e menor. Relembrando as fórmulas teremos que
Para o critério de Tresca
Em que sabemos que
E para o critério de Von Mises
Em que também sabemos que
Sabemos pelo enunciado que
Passo 2
Agora temos que determinar as tensões principais para podermos fazer o cálculo dos fatores de segurança
Sabemos que
Então
Também sabemos que
Logo
Passo 3
Como já temos esses valores, podemos facilmente determinar os valores das tensões máximas pelas fórmulas
Substituindo
O cisalhante máximo é muito simples, é o próprio valor do R que já calculamos
Passo 4
Agora que já temos todos os valores já podemos fazer as devidas substituições
Primeiro vamos calcular o fator de segurança pelo critério de Tresca.
Substituindo na nossa fórmula teremos que
Passo 5
Pelo critério de Von Mises teremos que o fator de segurança será
Sabemos que
E
Então nosso fator de segurança será
Resposta
Fator de segurança por Tresca
Fator de segurança por Von Mises
Exercício Resolvido #4
Elaboração própria
Um elemento possui resistência , sabendo que o fator de segurança de Tresca é igual a 1,2 e de Von Mises de 1,5 e que ainda Determine o maior valor de que cada critério nos permite ter.
Passo 1
Vamos primeiro descobrir o maior valor de que o critério de Tresca nos permite ter.
Temos que lembrar que
Em que sabemos que
E
Substituindo na nossa fórmula principal teremos que
Isolando o valor de teremos
Passo 2
Sabemos que o valor de cada termo da nossa equação para o critério de Tresca são
Passo 3
Vamos agora descobrir o maior valor de que o critério de Von Mises nos permite ter.
Temos que lembrar que
Em que também sabemos que
Substituindo cada termo na nossa equação principal
Sabemos que
Substituindo
Se resolvermos essa equação do segundo grau, teremos que
Ou
Como o valor de o único valor de que atenderá o que se pede será
Resposta
Pelo critério de Tresca
Pelo critério de Von Mises
Exercício Resolvido #5
Elaboração própria
Determine o fator de segurança para o elemento abaixo tanto por Tresca quanto por Von Mises sabendo que .
Passo 1
Sabemos que tanto o critério de Tresca, quanto o critério de Von mises dependem das tensões principais que agem nesse elemento, sendo em um necessário a tensão cisalhante máxima, e no outro, sendo necessário a tensão principal maior e menor. Relembrando as fórmulas teremos que
Para o critério de Tresca
Em que sabemos que
E para o critério de Von Mises
Em que também sabemos que
Sabemos pelo enunciado que
Passo 2
Como sabemos, para determinar as tensões principais em um elemento tridimensional sem ação de tensões cisalhantes, basta apenas organizar as tensões indo do maior valor para o menor valor, logo
Como já sabemos, para determinar o cisalhante máximo basta usar a fórmula
Passo 3
Agora vamos determinar o fator de segurança pelo critério de Tresca
Sabemos que
Substituindo na nossa fórmula teremos que
Passo 4
Pelo critério de Von Mises teremos que o fator de segurança será
Sabemos que
E
Então nosso fator de segurança será
Resposta
Fator de segurança por Tresca
Fator de segurança por Von Mises
Exercício Resolvido #6
Elaboração própria
Determine o fator de segurança para o elemento abaixo, sabendo que . Use o critério de tresca e de Von mises para isso.
Passo 1
Sabemos que tanto o critério de Tresca, quanto o critério de Von mises dependem das tensões principais que agem nesse elemento, sendo em um necessário a tensão cisalhante máxima, e no outro, sendo necessário a tensão principal maior e menor. Relembrando as fórmulas teremos que
Para o critério de Tresca
Em que sabemos que
E para o critério de Von Mises
Em que também sabemos que
Sabemos pelo enunciado que
Passo 2
Sabemos que como apresenta-se tensão cisalhante em alguns planos, estes não poderão ser considerados planos principais.
O que podemos afirmar é que o plano sem tensões cisalhantes é de fato um plano principal, podemos então afirmar que
Mas como determinar as tensões principais referentes aos outros planos?
Passo 3
Basta usarmos os conceitos aprendidos na aula de transformação de tensões.
Basta analisar o seguinte elemento infinitesimal dado pelos esforços que agem nos planos com cisalhante.
Agora é só determinar as tensões principais presentes nesse elemento infinitesimal.
Passo 4
Sabemos que para determinarmos as tensões principais precisamos usar
Que nos fornece a média das tensões
Que nós dá o cisalhante máximo que o nosso elemento foi submetido
A última fórmula é dada por
Que de fato nos fornece o valor das tensões principais
Sabemos que
Substituindo teremos que
Organizando teremos que
Mas também precisamos do valor de tensões cisalhantes máxima
Passo 5
Agora vamos determinar o fator de segurança pelo critério de Tresca
Sabemos que
Substituindo na nossa fórmula teremos que
Passo 6
Pelo critério de Von Mises teremos que o fator de segurança será
Sabemos que
E
Então nosso fator de segurança será
Resposta
Fator de segurança por Tresca
Fator de segurança por Von Mises