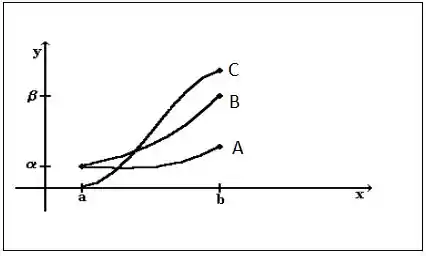
O método de Shooting para equações lineares é baseado na substituição de valor de fronteira, pelos resultados obtidos em e . Ele transforma um PVC em duas equações do tipo PVI. Analise o gráfico abaixo e relacione com os termos ou fórmulas dadas:
( )
( )
( )
Passo 1
Em um intervalo de a até b (nossa condição de contorno). Onde é solução de PVI-1 e é solução de PVI-2. Existe uma equação que mostra que podemos ter a solução do PVC com:
Avaliando as curvas no gráfico vemos que:
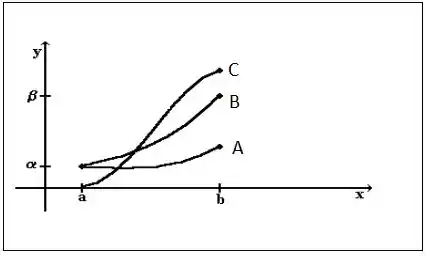
( A )
( C )
( B )
Resposta
( A )
( C )
( B )