Para estrutura abaixo, sabendo que à mesma possui a temperatura das fibras externas igual a e a temperatura das fibras internas igual a , determine a rotação dos pontos B e C.
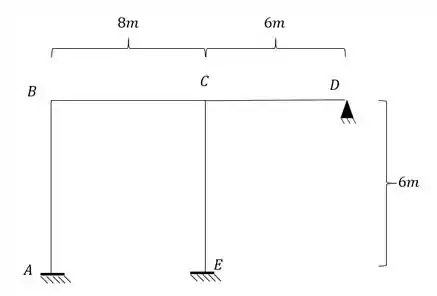
Passo 1
Antes de tudo precisamos saber a temperatura no da nossa estrutura, sabemos que se for diferente de zero, deveremos usar williot, se for igual a zero, teremos que usar as formulazinhas básicas que temos.
Com isso, basta desenharmos o nosso diagrama de temperatura, e vermos no que vai dar, sendo assim teremos que:
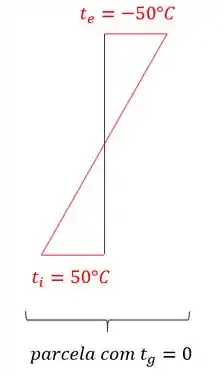
Com isso vemos que a nossa estrutura tem a temperatura no centro de gravidade igual a zero.
Logo as fórmulas que temos que usar são:
- Caso Bi-engastado
- Caso Engastado e apoiado
- Sabemos que os pontos A, E e D são indeslocáveis
- Sendo assim, os pontos B e C também serão considerados indeslocaveis.
- Dessa maneira não temos deslocabilidades externas
- Mas os pontos B e C podem rotacionar, e precisamos travar isso com uma chapa.
- Logo temos 2 deslocabilidades internas
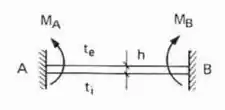
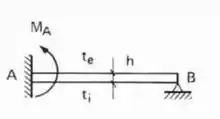
E pasmem, é só isso mesmo que fazemos quando o .
Mas ainda tem uma observação muito importante:
Os sinais dos momentos são feitos levando em consideração que , ou seja, que as temperaturas das fibras internas são maiores que as da externa.
E no nosso caso é exatamente isso que acontece, então podemos ficar tranquilos quanto a isso.
Passo 2
Sabendo qual é o nosso caso, precisamos agora definir as nossas deslocabilidades.
Sendo assim, desenhando a nossa estrutura, vamos ter que:
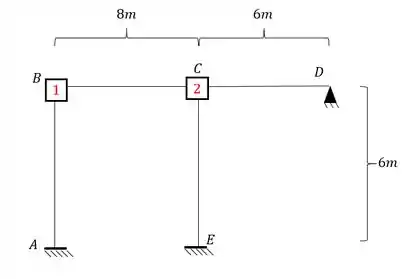
Passo 2
Determinado tudo isso vamos definir o valor de .
Sabemos que tanto a barra AD quanto a barra DC apresentam um engaste em uma ponta e uma chapa na outra, sendo assim, podemos considerar elas bi-engastadas, e para a barra bi engastada a equação é:
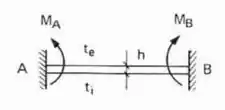
Mas a barra está em pé, o que faremos? Basta vira a figura.
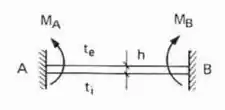
Assim podemos aplicar essa fórmula nas seguintes barras:
- AB
- BC
- CE
Fazendo isso teremos que:
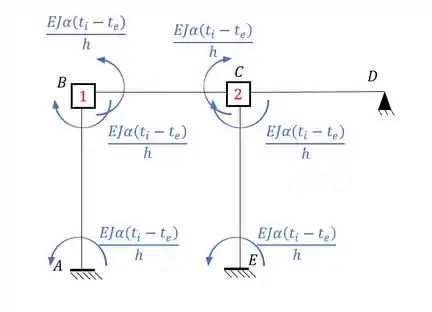
Como essa fórmula independe do comprimento, podemos calcular uma das equações e depois substituir na estrutura respeitando o sinal.
Substituindo na estrutura teremos que:
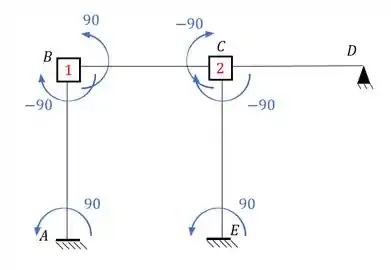
Para a barra CD, podemos ver que de um lado temos a chapa e do outro temos um apoio, ou seja, podemos considerar essa barra do tipo engastada e apoiada, e a fórmula a ser usada nela é:
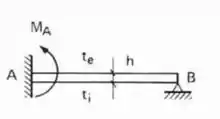
E aplicando isso a nossa estrutura teremos que:
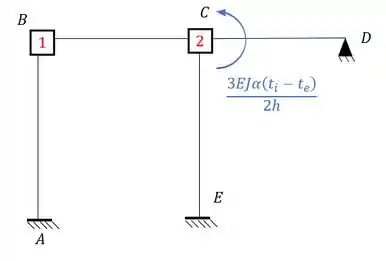
Perceba que para respeitar a regrinha de o momento sempre sair das fibras inferiores e ir pra superiores, nós invertemos o sentido do momento para ficar tudo certinho.
Substituindo na fórmula teremos que
Olhando a estrutura com todos os momentos teremos que:
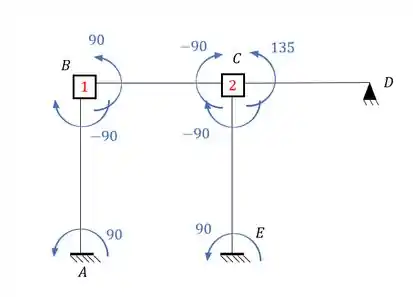
Assim teremos que a rigidez total em D será dado por:
Passo 3
Agora precisamos determinar a parcela referente a rotação que pode ser unitária ou podemos usar o conceito de rigidez relativa:
- e
- e
Sabemos aqui que temos que rotacionar a chapa 1, e sabemos que se fizermos isso nos sentido anti-horário, sempre teremos os nossos momentos positivos, sendo assim teremos a seguinte tabela a ser usada para as barras 2 e 3 respeitando o caso biengastado ou engastado e apoiado:
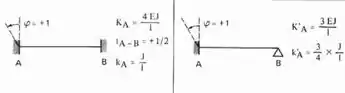
E rotacionando a chapa 1 e aplicando as equações teremos:
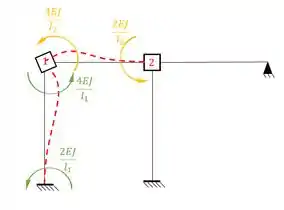
Veja que temos:
Parece meio complicado calcularmos isso, certo? Então podemos usar o nosso fator para rigidez relativa:
E assim teremos:
Como já vimos no início dessa aula, , substituindo teremos que:
Veja também que:
Como já usamos o fator de rigidez relativa, devemos continuar usando ele, e perceba que não podemos mudar mais, se usamos em um, temos que usar o mesmo em todos, sendo assim teremos que:
E assim teremos:
Como já vimos no início dessa aula, , substituindo teremos que:
Passo 5
Determinando o resto do sistema teremos que:
Sabemos aqui que temos que rotacionar agora a chapa 2, e sabemos que se fizermos isso nos sentido anti-horário, sempre teremos os nossos momentos positivos, sendo assim teremos a seguinte tabela a ser usada para as barras 2 e 3 respeitando o caso biengastado ou engastado e apoiado:
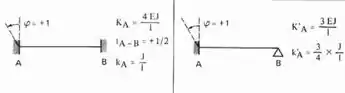
E rotacionando a chapa 2 e aplicando as equações teremos:
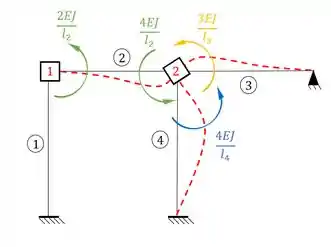
Veja que temos:
Parece meio complicado calcularmos isso, certo? Então podemos usar o nosso fator para rigidez relativa:
E assim teremos:
Como já vimos no início dessa aula, , substituindo teremos que:
Veja também que:
Como já usamos o fator de rigidez relativa, devemos continuar usando ele, e perceba que não podemos mudar mais, se usamos em um, temos que usar o mesmo em todos, sendo assim teremos que:
E assim teremos:
Como já vimos no início dessa aula, , substituindo teremos que:
Passo 4
Agora que já fizemos a parte mais difícil, basta montarmos o nosso sistema de equações que será:
Resolvendo esse sistema teremos que:
Perceba que os valores de deformações calculados já são as deformações de rotação dos pontos pedidos no enunciado, ou seja, o ponto B (referente a ) e o ponto C (referente a .
Porém tome cuidado, porque para calcularmos essas deformações usamos um conceito de rigidez relativa, que é exatamente o fatorzinho que usamos pra facilitar o cálculo, que é dado por:
Então basta usarmos esse fator para descobrirmos a deformação verdadeira: