Potência e Eficiência
Produzido por Marcelo AlvesTeoria
Potência
A gente já viu que as bombas dão energia, carga pra um líquido, certo? Agora imagina que eu tenho que dar pra um líquido lá de carga. Se tiver passando do líquido na bomba ou , a carga TOTAL que eu tenho que fornecer para aquela vazão é diferente.

A potência da bomba é uma medida da taxa de carga que eu estou fornecendo efetivamente pra uma determinada vazão mássica ou volumétrica passando por uma bomba:
Eficiência ou Rendimento
Repara que quando eu falei de potência, disse que ela era a taxa de carga EFETIVAMENTE fornecida ao líquido. Isso é quase que um spoiler haha Deixa eu te explicar melhor como ocorre essa transferência.

Temos que fornecer uma determinda energia pro motor da bomba e ela vai usar essa energia pra girar o impelidor, por exemplo, no caso de turbobombas. O que entra em contato com o fluido e transfere energia pra ele é o impelidor. Acontece que nem toda energia transferida pro motor é repassada para o fluido. Daí surge eficiência:
Ou seja, eficiência ou rendimento da bomba é uma razão entre a potência da bomba e a potência do motor. Rendimento é sempre essa ideia: o que entrega dividido pelo que recebeu.
Curva de eficiência
Assim como a carga fornecida por uma bomba varia por uma bomba varia com a vazão, a eficiência também varia e os fabricantes nos fornecem esses gráficos.
Um ponto muito importante dessa curva é o , que é o best efficiency point, isto é, o ponto de melhor eficiência.
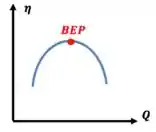
Quanto mais próximo desse ponto a operação for, melhor, mas sem sacrificar a carga necessária ao projeto.
Curvas características de famílias de bombas
Nós já vimos, ao longo das teorias sobre bombas, que há mudança das variáveis nas bombas com a alteração da vazão; vimos também que o fabricante fornece os gráficos das variáveis relacionadas as bombas. Acontece que eles não dão 500 gráficos, eles juntam tudo em uma coisa só. Dá uma olhada em um:
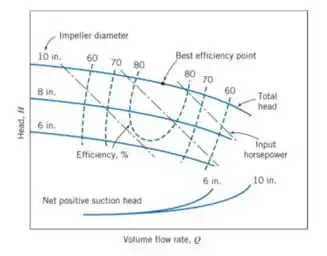
Repara que nesse gráfico temos como tirar informações para 3 bombas diferenciadas pelo diâmetro do impelidor delas . E as informações que podemos extrair é:
- Head , que é a carga fornecida
- Curvas de eficiência e a localização do BEP
- Input horse-power, isto é, a potência requerida pelo motor
- Curvas de NPSH, que no caso é o REQUERIDO, já que esse é dependente apenas da bomba
Quanto à eficiência e potência requerida pelo motor, podemos fazer interpolação linear pra encontrar valores intermediários entre as curvas deles.
Eficiência ou Rendimento
Curva de eficiência
Curvas características de famílias de bombas
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria
Sobre potência e eficiência, é correto afirmar que:
- Toda potência fornecida pelo motor é sempre transferida ao fluido
- A energia total transferida ao fluido por unidade de tempo é a potência da máquina de fluxo
- Buscamos sempre a máquina de fluxo com menor eficiência
- Eficiência alta é o principal critério ao avaliar uma bomba
Passo 1
Bora analisar as alternativas uma por uma. A primeira é:
- Toda potência fornecida pelo motor é sempre transferida ao fluido
- A energia total transferida ao fluido por unidade de tempo é a potência da máquina de fluxo
- Buscamos sempre a máquina de fluxo com menor eficiência
- Eficiência alta é o principal critério ao avaliar uma bomba
Isso só ocorreria se a eficiência fosse , certo? Lembra que a fórmula de eficiência é:
Daí:
E é a potência efetivamente transferida ao fluido.
Passo 2
SIMMMMM! É exatamente a definição de potência que a gente viu na teoria.
E está escrito “potência da máquina de fluxo” porque potência é um conceito geral, NÃO vale só pra bombas e, como já vimos, bombas só servem pra fluidos incompressíveis. Mais pra frente vamos ver máquinas de fluxo pra fluidos compressíveis :)
Bora continuar vendo as outras alternativas
Passo 3
Não, né? Queremos sempre a MAIOR eficiência possível.
Se a eficiência for baixa, significa que está havendo desperdício de grande parte da energia fornecida pelo motor e não queremos isso... Lembra que:
Passo 4
Eficiência alta é muito interessante, pois está havendo menor perda de energia, mas NÃO é o principal critério ao selecionar uma bomba. Os principais são escolher uma bomba que disponibilize vazão de operação próxima à exigida pelo projeto E que NÃOOOO haja cavitação.
Depois de garantir esses dois pontos, analisamos a eficiência e escolhemos a bomba com maior eficiência dentre as que “passaram” no primeiro teste.
Pensa só, não adianta ter eficiência alta se a bomba estiver cavitando (daí está sendo destruída), por exemplo.
Resposta
- A energia total transferida ao fluido por unidade de tempo é a potência da máquina de fluxo
Exercício Resolvido #2
Elaboração própria
Uma corrente gasosa necessita ganhar de carga. Sabendo sua vazão volumétrica , podemos afirmar:
- A potência necessária é
- Não é necessário conhecer a densidade da corrente para determinar a potência
- A vazão mássica também vale
- Com estes dados, não se pode calcular a potência sem se conhecer a densidade
Passo 1
O enunciado fala de uma corrente GASOSA e diz que sua vazão VOLUMÉTRICA vale ; fala também que a corrente precisa ganhar de carga .
Temos algumas frases pra analisar. Bora uma por uma.
Passo 2
- A potência necessária é .
- Não é necessário conhecer a densidade da corrente para determinar a potência
- A vazão mássica também vale
- Com estes dados, não se pode calcular a potência sem se conhecer a densidade
Lá na teoria, a gente viu que a fórmula de potência é:
Como temos a vazão volumétrica, trabalhamos com:
OK, temos e e é a gravidade, então temos como saber. Mas e a densidade do gás ???
Repara que como não temos nem a densidade e nem formas de calcular a densidade (já que não sabemos qual é o gás e suas condições), NÃO temos como calcular a potência só com os dados fornecidos pelo enunciado.
Finge que você não viu que a resposta é a letra d e bora ver porque as outras alternativas estão erradas.
Passo 3
A gente acabou de ver na letra que, como temos a vazão volumétrica, precisamos da densidade pra calcular a potência.
Passo 4
NÃOOOOOOOO. Vazões mássica e volumétrica são coisas completamente diferentes. Massss, usando a densidade, podemos relacioná-las:
É importante não confundir essas duas vazões e lembrar que a vazão MÁSSICA permanece constante, mas a volumétrica pode variar e, por isso, precisa-se usar e medidos nas mesmas condições sempre.
Passo 5
E, como já vimos no passo 2, tendo a vazão volumétrica, mas sem a densidade, NÃO conseguimos calcular a potência pois:
Resposta
d) Com estes dados, não se pode calcular a potência sem se conhecer a densidade
Exercício Resolvido #3
Elaboração própria
Uma vazão mássica de água pura à passa por uma bomba e ganha de carga. Calcule a eficiência da bomba, sabendo que a potência consumida pelo motor é .
Passo 1
Primeiro de tudo: já temos a vazão mássica então não precisamos nos preocupar com densidade, correto? Não vamos precisar da informação da temperatura pra nada.
Continuando, o enunciado pede pra calcular a eficiência, que é dada por:
Ainda não temos a potência fornecida pela bomba , então a primeira coisa a fazer é calculá-la.
Passo 2
Lá na teoria, a gente viu que a fórmula de potência é:
Como temos a vazão mássica, trabalhamos com:
Vou trabalhar no SI, já que a vazão mássica e carga já estão nesse sistema de unidades. Daí, usamos:
Substituindo os valores:
Passo 3
Agora sim podemos calcular a eficiência:
No passo anterior calculamos:
E o enunciado nos deu que:
Fazendo a conta:
Resposta
Exercício Resolvido #4
Elaboração própria
Assumindo que para uma determinada bomba a curva de eficiência possa ser descrita, em base unitária, por:
Com em .
Calcule a eficiência e a vazão do ponto de maior eficiência .
Passo 1
Nessa questão, precisamos encontrar o BEP, que é o ponto de maior eficiência. Temos a curva de eficiência versus vazão volumétrica :
Pra resolver essa questão, vamos ter que usar justamente o fato de o ponto de maior eficiência ter a maior eficiência haha

Pensa só: nos é dada uma parábola com concavidade para baixo (já que um número negativo multiplica o termo ao quadrado) como curva de eficiência; como queremos o ponto de maior eficiência, estamos atrás do ponto de máximo dessa parábola. Daí é só derivar e igualar a zero que achamos o BEP

Passo 2
Bora derivar essa função aí em termos de :
Igualando a derivada a zero:
Isolando :
Uma parte já foi; já achamos a vazão do BEP. Agora só falta achar qual a eficiência no BEP. Pra isso, é só jogar esse valor da do BEP na curva de eficiência e calculá-la:
Prontinho.
Resposta
Vazão volumétrica no BEP:
Eficiência no BEP:
Exercício Resolvido #5
Elaboração própria
Uma bomba centrífuga opera com uma vazão de e fornece de carga ao fluido.
- Calcule a potência da bomba
- Sabendo que a potência consumida pelo motor é de , calcule a eficiência da bomba.
Dado: o fluido possui densidade de
Passo 1
Tem uma bomba e a gente sabe a vazão volumétrica passando por ela e a carga fornecida ao fluido.
Como também foi dada a densidade do fluido, , podemos aplicar a fórmula e calcular a potência:
Como o que temos é vazão volumétrica:
Substituindo os valores:
Repara que nem todas as unidades estão compatíveis; com exceção da vazão, as unidades estão no SI, então vou converter a vazão pro SI também.
Voltando pra potência:
Passo 2
- Sabendo que a potência consumida pelo motor é de , calcule a eficiência da bomba.
Pra calcular eficiência, é só lembrar que é o que entrega dividido pelo que recebeu. Isto é:
A potência da bomba, , a gente já calculou no primeiro item:
E a potência do motor é dado do enunciado:
Então o nosso trabalho é só fazer uma divisão haha