NPSH e Cavitação
Produzido por Marcelo AlvesTeoria
Introdução à Cavitação
A gente viu no tópico anterior que bombas fornecem energia em forma de pressão a um líquido, mas NÃO necessariamente aumentam a velocidade do fluido. Isso é sim verdade de um ponto de vista global, vendo-se antes e depois da bomba. Mas para falar de cavitação, precisamos olhar pra dentro da bomba.

O fluido é sugado pra dentro da bomba e acelerado localmente. A entrada é perpendicular ao rotor e depois ele fica em um movimento circular em direção à saída, bocal de recalque. Esse aumento de velocidade contribui pra maior queda de pressão do fluido.
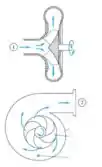
Dentro da bomba, a pressão do fluido pode diminuir até sua pressão de vapor e aí ocorre a ebulição do líquido e formação de bolhas. Só que essa queda de pressão é local; depois, essas bolhas são transportadas para regiões com .

Quando chega em uma região em que , essas bolhas colapsam, isto é, voltam a líquido, liberando energia. Esse fenômeno é denominado CAVITAÇÃO e gera ruído, vibrações, erosão nos equipamentos e modificação da curva característica da bomba.
“Equacionando” a Cavitação
A gente já viu que, nem tudo são flores; antes de ganhar pressão na bomba, o líquido perde pressão e, para não cavitar, tem que sempre. Então é razoável dizer que tem uma condição mínima que o líquido precisa ter ao chegar na bomba, certo?

Um ponto muitooo importante quando se fala em cavitação é o “olho” do impelidor, que é o ponto em que o líquido (que entra perpendicular ao impelidor) “dá de cara” com o impelidor.
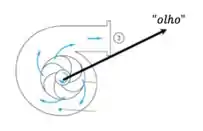
Esse é o ponto mais crítico, o que o líquido fica com menor pressão. Bora fazer um balanço de energia entre a entrada da bomba (bocal de sucção) e o olho:
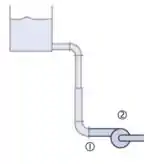
Mas a entre 1 e 2 a bomba ainda não deu nenhuma carga então ; além disso, . Daí:
E repara que surgiu um termo novo: . Esse termo é referente ao sistema rotativo ao qual o fluido está submetido no olho do impelidor.
Mas não se preocupa com esse termo não; já te explico o porquê haha Bora lá; o que queremos é que , mas, no limite, . Fazendo isso, dividindo tudo por e rearranjando:
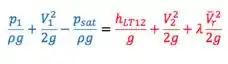
Primeiro, eu considerei que e , isto é, regime turbulento, o que é bem razoável. Além disso, esses termos não estão coloridos à toa: eles são o NPSHD e NPSHR, respectivamente.

E, antes de continuar falando de cavitação, precisamos parar e falar desses dois caras aí.
NPSH
Antes de qualquer coisa, o que significa NPSH? Isso é uma sigla em inglês para “net positive suction head”, que em português é “carga de sucção líquida positiva”. E vimos que tem NPSHD e NPSHR, que são:
- O NPSH Disponível depende do fluido e do sistema em questão, já que depende da pressão em 1, da do líquido e da velocidade em 1.
- Já o NPSH Requerido depende da bomba e é medido pelo fabricante! Daí o não precisar se preocupar com aquele termo com .
- Aumentando , NPSHD diminui porque, embora aumente, as perdas de carga antes da sucção aumentam muito e fazem cair muito, mais do que o aumento de .
- Aumentando , NPSHR aumenta porque aumenta .
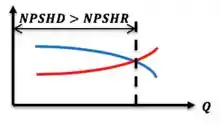
- Diminuir a vazão (olha o gráfico aí em cima). Ao fazer isso, o NPSHD aumenta porque diminuem as perdas de carga
- Diminuir a temperatura. Isso vai diminuir a e, como ela está multiplicada por no NPSHD, o NPSHD vai ficar maior.
- Aumentar em relação ao reservatório porque aí o líquido chega com maior.
- Diminuir porque aí diminui-se a perda de carga e aumenta a pressão com que o líquido chega na entrada da bomba, .
- Aumentar o diâmetro da tubulação, assim diminui-se a perda de carga e, por consequência, aumenta .
Algo que precisamos entender, também, é o comportamento desses dois NPSH com o aumento da vazão :


Evitando Cavitação
Agora que já entendemos o que são esses NPSH, bora voltar para aquele equacionamento de cavitação. Chegamos, no limite de cavitação, em:
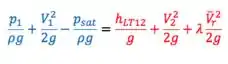
Para que NÃO haja cavitação, o NPSH Disponível tem que ser MAIOR que o Requerido. Desta forma, o líquido tem energia suficiente para garantir que sempre.
Medidas para evitar cavitação
Já vimos que para não cavitar, .
Ok, mas você vai chegar pro líquido e falar: “Fica com o NPSHD maior que o NPSHR, hein” ? Precisamos dar soluções palpáveis e vou listar algumas aqui: