Sedimentação
Teoria
Introdução
Antes de qualquer coisa, sedimentadores também podem ser chamados de espessadores (quando seu interesse é no líquido) ou clarificador (quando seu interesse é no líquido), mas é tudo a mesma coisa haha
Algumas coisas que você precisa saber sobre sedimentadores:
- Operação contínua
- A força motriz pra separação é apenas a gravidade
- São equipamentos bem grandes e operam sempre em regime laminar
“Como sedimentadores funcionam?”
A gente coloca a suspensão a ser separada por cima do tanque; as partículas vão sedimentando e se acumulando no fundo e o líquido em cima vai ficando “limpo”, sem partículas, e extravasa do tanque. Por baixo, retiramos um concentrado em partículas, um lodo.
Zonas em um Sedimentador
Como te falei, as partículas vão se acumulando mais para o fundo; quando olhamos o sedimentador, temos zonas:
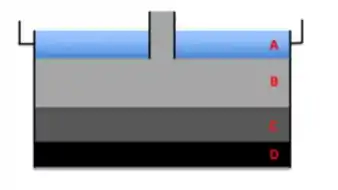
Como projetar um Sedimentador?
Então, você vai precisar dos resultados de um experimento, que é o teste de proveta. O único requisito pra ele é que use uma suspensão com a mesma concentração volumétrica que a da suspensão a ser usada no sedimentador; o resto dá pra corrigir.
Colocamos a suspensão na proveta e, a partir de um instante até um tempo infinitamente grande, o perfil das zonas na proveta fica assim:
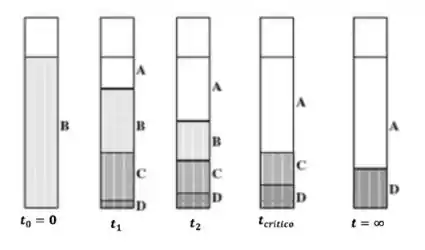
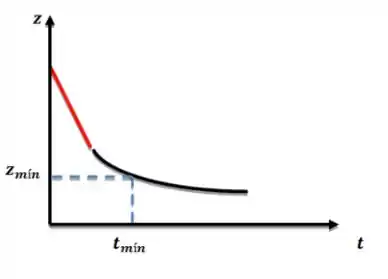
O que vamos extrair desse experimento é a altura da interface de líquido clarificado com o tempo. Ela fica assim:
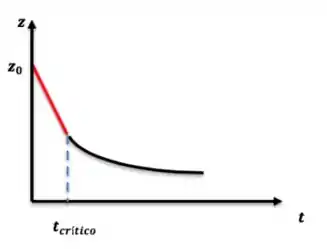
O ponto mais importante em relação a teoria envolvida nessa curva é esse trecho em vermelho, que é LINEAR. Isso ocorre porque até , a altura da interface da zona muda devido à sedimentação das partículas na zona , que possui concentração constante e, por isso, velocidade terminal das partículas constante!
Guarda esse experimento aí que depois vamos extrair mais coisa dele, ok?
Algumas relações importantes
Bora analisar um nível qualquer no sedimentador. O sólido só desce e, conforme ele desce e vai comprimento o líquido, parte do líquido sobe, puro . Daí, representando as vazões e concentrações num sedimentador, incluindo o nível :
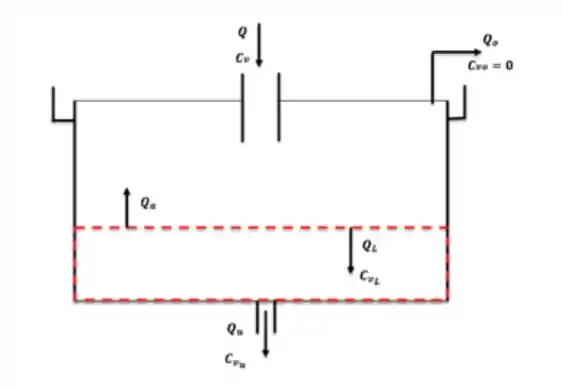
Fazendo um balanço de massa pra sólidos (que se mantém constantes ao longo do sedimentador), podemos achar relação entre :
Posso cortar os :
Daí:
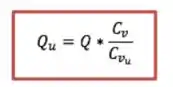
Fazendo balanço para o líquido naquela envoltória tracejada em vermelho:
Depois de algumas manipulações:
Em que é a área transversal do sedimentador. Sendo que:
E pensa comigo: pra ter sedimentação, a velocidade de sedimentação da partícula tem que ser maior do que a velocidade de ascensão do líquido né. No limite, seria igual.
No limite, temos a igualdade e aí, chegamos na equação de trabalho em sedimentação:
Dessa equação de trabalho, também podemos tirar uma fórmula para a capacidade, que é quanto de líquido claro recuperamos, que é o .
Cálculo da área do sedimentador
Agora vamos aprender como fazer as contas pra projetar um sedimentador.
Na hora de calcular a área do sedimentador, sempre vamos superdimensionar. Calculamos uma área mínima e depois aplicamos fatores de correção para aumentar a área para caso ocorram variações na alimentação.
Em que é o tempo pra atingir a altura no teste de proveta.
E pra calcular
Como te disse, sedimentadores são superdimensionados. A área que vamos usar na realidade é a área de projeto
Se nada for falado, EU uso o valor médio, isto é, . Quanto a :
Em que é o diâmetro calculado a partir da .
Correção com a Temperatura
Se . Não vou mostrar todo o passo a passo, mas acredita em mim:
Outra relação que podemos usar é:
Cálculo da altura do sedimentador
Bora lembrar daquelas zonas do sedimentador:
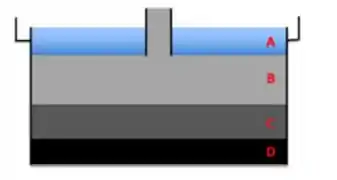
De fórmula para altura, só temos uma, que é pra calcular as alturas de :
Em que
Quanto a , tem as recomendações do livro do Perry:
O meu professor falava pra usarmos os valores médios desses intervalos. E, só pra constar haha:
Vou te mostrar agora como achar certinho .
Cálculo do
Você tem que traçar tangentes às duas partes “constantes” da curva , isto é, na parte linear e na parte em que a altura fica com variação mais ou menos constante. Do ponto que elas se encontram, você traça uma bissetriz e terá o quando ela encontrar a curva. Olha só:
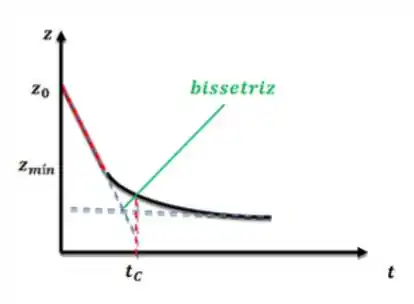
Cálculo de
Aqui também trabalhamos com tangente, mas, agora, a partir do (exatamente o mesmo que vimos no cálculo da área), traçamos uma tangente à curva . Do ponto que a tangente encostar na curva, tiramos :
Como projetar um Sedimentador?
Algumas relações importantes
Cálculo da área do sedimentador
Correção com a Temperatura
Cálculo da altura do sedimentador
Cálculo do t C
Cálculo de t u
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria
Explique a importância da suspensão a ser separada em um sedimentador ser injetada lentamente. Além disso, aponte qual parte do processo de sedimentação pode ser enxergado como escoamento em meio poroso e diga o porquê.
Passo 1
Vamos por partes. Primeiro temos que explicar porque temos que injetar a suspensão lentamente no sedimentador.
Lembra que o sedimentador separa os sólidos apenas pela força gravitacional? Além disso, sabemos que injetamos a suspensão continuamente por cima e as partículas vão “descendo” e acumulando no fundo do sedimentador enquanto o líquido limpo extravasa por cima.
Precisamos injetar a suspensão lentamente por que, do contrário, iria haver ressuspensão de partículas e não conseguiríamos obter líquido limpo. Tipo, pensa num copo de achocolatado. Se você deixa ele lá parado por muito tempo, acaba acumulando um líquido mais escuro no fundo, mas se você começa a movimentar muito o copo, ele vai se espalhando mais pra cima... é tipo essa ideia.
Passo 2
Quanto a parte de escoamento em meio poroso, ela ocorre justamente lá no final do sedimentador. Pensa só, lá na teoria vimos que injetamos a suspensão e os sólidos vão descendo e o líquido limpo vai subindo e extravasando por cima.
Logo que injetamos a suspensão, ok, ela está “diluída”, mas conforme os sólidos vão chegando mais pra baixo do sedimentador e já estão mais concentrados, o líquido contido nele tem cada vez mais dificuldade para passar pelos sólidos e subir. Chega um ponto que os sólidos estão tão concentrados, que é como um escoamento em meios porosos.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #2
Elaboração própria
Calcule a vazão de lodo num sedimentador sabendo que a vazão de alimentação é , e .
Passo 1
Essa é bem aplicação de fórmula mesmo; lá na teoria vimos que fazendo balanço de massa para sólidos no sedimentador, dá pra chegar em:
Repara que nessa fórmula aparecem concentrações volumétricas e isso é porque nos referimos à essa concentração no desenvolvimento lá na teoria. Como aparece uma razão de concentrações e os fatores de conversão seriam os mesmos para as duas, podemos escrever:
Substituindo os valores:
Resposta
Exercício Resolvido #3
Determinar a área, a altura e a vazão de concentrado de um sedimentador capaz de tratar de uma suspensão aquosa de barita, sabendo que se espera obter uma relação de .
Um teste de proveta, realizado à mesma concentração e temperatura de alimentação, produziu o seguinte resultado:
Passo 1
O primeiro passo que temos que fazer é pegar essa tabela de e transformá-la em um gráfico pra podermos trabalhar.
Vamos nas contas precisar de , e ; no caso do , já conseguimos determinar direto com a bissetriz nas tangentes, saca só:
Para os outros tempos, primeiro precisamos calcular :
Do gráfico:
Passo 2
Para calcular a área, calculamos a área mínima e depois aplicamos os fatores de correção.
Usando o metro como unidade de comprimento, e :
Mas:
Se nada for falado, EU uso o valor médio, isto é, . Quanto a :
Em que é o diâmetro calculado a partir da .
Daí:
Então:
Passo 3
Precisamos das alturas das quatro zonas:
Para , tem as recomendações do livro do Perry:
O meu professor falava pra usarmos os valores médios desses intervalos. Daí:
Para :
Como:
Resposta
Exercício Resolvido #4
Determinar o diâmetro e a altura de um sedimentador para operar com de uma suspensão aquosa de barita ( ) a . A concentração de sólidos na alimentação é de de suspensão e o lodo final deve ter de suspensão. Ensaio de proveta a conduziu ao seguinte resultado:
Passo 1
Primeiro de tudo: o enunciado deu concentrações em massa por volume , mas precisamos de concentrações volumétricas ! Daí, dividiríamos pela densidade para converter essa massa do numerador pra volume:
Escrevi isso só pra chamar sua atenção pra esse detalhe, mas na real nem vamos precisar fazer isso nessa questão porque vamos trabalhar com razão de concentrações. Espera aí que vou te mostrar isso melhor.
Antes, bora transformar esses dados de em um gráfico para podermos trabalhar:
Passo 2
Bora começar com a área; para calcular a área, calculamos a área mínima e depois aplicamos os fatores de correção.
Precisamos calcular o pra poder tirar, do gráfico, .
E daí o não precisar converter as unidades de concentração pra esse problema, mas bora mostrar que a gente sabe:
Daí:
Do gráfico:
Agora já podemos calcular :
Usando metro e hora:
Mas:
Se nada for falado, EU uso o valor médio, isto é, . Quanto a :
Em que é o diâmetro calculado a partir da .
Daí:
Então:
Mas o que o enunciado pediu foi o diâmetro:
Passo 3
Precisamos das alturas das quatro zonas:
Para , tem as recomendações do livro do Perry:
O meu professor falava pra usarmos os valores médios desses intervalos. Daí:
Para :
Ainda não calculamos . Bora lá:
Eu li
Eu li
Convertendo esses dois tempos para hora:
Daí:
Novamente, nem precisamos converter as concentrações por se tratar de uma divisão; os fatores de conversão seriam os mesmos em cima e embaixo nesse exemplo.
Como: