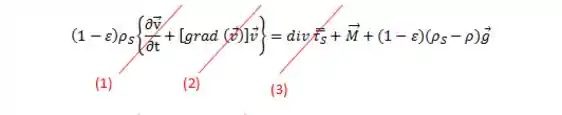Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Fluidização

Ver Todos os Exercícios

Teoria

Introdução

Bora pensar em um bando de partículas paradas lá de boas na vida. Aí você começa a fazer um fluido passar por elas lentamente: vai rolar um escoamento em meio poroso. Ok!

Aí imagina que você resolve usar uma vazão absurda do fluido! O que vai acontecer é que as coitadas das partículas vão ser arrastadas e você vai perdê-las!

Mas se você usar uma vazão intermediária, você pode obter um leito fluidizado, que é quando as partículas estão se movimentando no leito, mas não saem de uma certa região, não saem do equipamento.

Queda de pressão em leitos fluidizados

Para chegar numa expressão para queda de pressão, vamos ter que usar a equação do movimento e olhá-la tanto para o fluido como para o sólido. Ah! O leito fica na vertical hein, então vamos ter que considerar o termo que tem gravidade. Saca só:

  • Para o fluido:

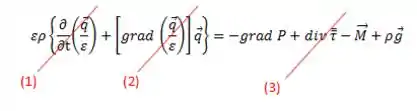
  1. Considerando estado estacionário
  2. Considerando q constante
  3. Considerando forças viscosas desprezíveis face à força M

Daí:

0 = - d P d z - M → + ρ g →

Guarda isso. E ah! A pressão em uma dada altura do leito é constante; só varia com a altura e por isso só sobra d P d z do gradiente.

  • Para o sólido:

    1. Considerando estado estacionário
    2. De modo global, as velocidades médias das partículas não mudam; elas NÃO saem do leito
    3. Considerando forças viscosas desprezíveis face à força M

    Daí:

    0 = M → + 1 - ε ( ρ S - ρ ) g →

    Guarda essa equação também. Na real, vou usar é agora haha. O M → é um só e achamos duas equações envolvendo ele; isolando-o em cada uma das equações:

    M = - d P d z - ρ g M = 1 - ε ( ρ S - ρ ) g

    Num leito fluidizado, o fluido entra por baixo e sobe. Daí vai contra a gravidade e por isso já substitui aí em cima g → = - g

    Mas M é um só daí posso igualar essas equações:

    - d P d z = 1 - ε ρ S - ρ g + ρ g

    O leito tem comprimento L ; fazendo separação de variáveis e integrando isso de 0   a   L , que corresponde respectivamente a P 0   e   P L .

    - ∫ P 0 P L d P = ∫ 0 L 1 - ε ρ S - ρ g + ρ g

    Lembrando que P L < P 0 já que o fluido perde pressão ao atravessar o leito. Usando ∆ P = P 0 - P L e multiplicando e dividindo o lado direito pela área de seção transversal do tubo, chegamos em:

    ∆ P = 1 - ε ρ S g A L + ε ρ g A L A

    Ufa! Pronto! Chegamos! Agora repara em uma coisa:

  • O primeiro termo do numerador é o peso dos sólidos, 1 - ε ρ S g A L
  • O segundo termo do numerador é o peso de fluido, ε ρ g A L

    • Então podemos escrever:

    ∆ P = P e s o   d o   l e i t o A

    Quando a fluidização é feita com gás: P e s o   d e   s ó l i d o s ≫ P e s o   d e   g á s , aí podemos simplificar por:

    ∆ P = P e s o   d e   s ó l i d o s A

    Curva de Histerese

    Histerese é quando os caminhos de ida e volta de alguma coisa não são iguais. Ocorre histerese em fluidização de um leito que estava parado: as partículas paradas tendem a ir se compactando e, quando você começar a injetar fluido, a resistência vai ser maior; uma vez que você fluidiza o leito, e resolver parar (e depois pode até refluidizar), vai percorrer um caminho com quedas de pressão menores:

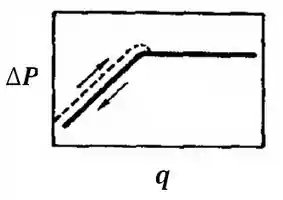
    A explicação disso é muitoooo simples: o leito fica mais fofo haha Pensa quando você vai colocar café solúvel num potinho pra guardar; às vezes o recipiente enche e você ainda tem café pra guardar, aí você dá umas batidinhas pra compactar o café, né? A mesma coisa acontece nos leitos haha.

    Velocidades Mínima e Máxima de fluidização

    Bora começar pela máxima que é mais simples: q m á x é a velocidade terminal da menor partícula que compõe o leito, porque qualquer velocidade maior que isso iria arrastar partículas.

    Para achar uma expressão pra velocidade mínima, usamos a equação de M que achamos da aplicação da equação do movimento para sólidos e da equação de Forchheimer (que vale pra qualquer escoamento em meio poroso né):

    M = 1 - ε ( ρ S - ρ ) g M = μ K 1 + C K ρ q μ q

    Igualando as duas:

    μ K 1 + C K ρ q μ q = 1 - ε ( ρ S - ρ ) g

    Essa equação daí vale pra QUALQUER ponto da fluidização.

    Para o caso de escoamento darcyano, C = z e r o . Aí, para escoamento Darcyano:

    μ K q = 1 - ε ( ρ S - ρ ) g

    Usando o modelo de Kozeny-Carmán para K :

    K = Φ d - 2 ε 3 36 β 1 - ε 2

    Substituindo:

    μ q f 36 β 1 - ε f 2 Φ d - 2 ε f   3   = 1 - ε f ( ρ S - ρ ) g

    Esse subscrito f indica uma condição qualquer de fluidização. Podemos escrever, também, para as condições de mínima fluidização ( m f ) . E podemos relacionar as duas:

    ε f   3 1 - ε f = q f q m f . ε m f   3 1 - ε m f

    Guarda essa fórmula com carinho.

    Outra coisa que podemos saber é usar aquela expressão pra massa de sólidos no leito e escrevê-la para f e m f . Como a massa no leito nessas duas condições é constante, chegamos em:

    L f L m f = 1 - ε m f 1 - ε f

    Outra fórmula pra você guardar com carinho haha

    Potência consumida na fluidização

    A fluidização pode ser com líquido ou gás.

    • Para fluidização com líquido:

      • P o t = ρ g Q W b η

      Em que η é a eficiência da bomba; o resto a gente já viu.

    • Para fluidização com gás

    Considerando evolução isentrópica de gás ideal:

    P o t = γ γ - 1 P 2 Q 2 1 - P 1 P 2 γ - 1 γ . 1 η

    Em que:

    γ = C p C v

    E η é a eficiência do soprador.

    NÃO se assusta com a fórmula. Ela é feia mas não é brava. E ah! Os subscritos " 1 " são relativos à entrada do soprador e os " 2 " à saída.

    E quando usamos gás como um fluido, tem algo importante a lembrar: usamos um distribuidor na entrada do leito! Na maioria das vezes, desprezamos a perda de carga da saída do soprador até a entrada do distribuidor; se isso for considerado:

    P e n t r a d a   d o   d i s t r i b u i d o r = P 2

    Depois do distribuidor começa o leito e isso está associado à uma pressão P 0 , como chamei lá em cima. Daí:

    ∆ P d i s t r i b u i d o r = P 2 - P 0

    Na hora de fazer o projeto, ainda não vamos conhecer exatamente qual distribuidor vamos usar; para fazer uma estimativa da queda de pressão nele, há as recomendações de Kunii-Levenspiel:

    ∆ P d i s t r i b u i d o r = 0,1 . ∆ P l e i t o       s e       0,1 . ∆ P l e i t o ≥ 3500   P a   ∆ P d i s t r i b u i d o r = 3500   P a       s e     0,1 . ∆ P l e i t o < 3500   P a

    Curva de Histerese

    Velocidades Mínima e Máxima de fluidização

    Exercícios Resolvidos

    Exercício Resolvido #1

    Elaboração própria

    Calcule o Δ P do leito fluidizado formado adicionando-se 100 kg de zeólita ( d   =   100   µ m , ρ S   =   2,5   g / c m 3   e   ϕ   =   0,8 ) a uma coluna com 30   c m de diâmetro e q m f = 1,61   c m / s . Sabe-se que o fluido tem as propriedades do ar a 500   ° C   e   1   a t m e que a altura nas condições de fluidização mínima é 1,40   m .

    Passo 1

    Existem três formas de calcular a queda de pressão em um leito fluidizado.

    Experimentalmente, constatou-se que:

    Δ P ≅ P e s o   d o   l e i t o A

    Ou seja, a perda de carga é igual ao peso do leito dividido pela área transversal do leito.

    Por outro lado, existem equações que relacionam a perda de carga às condições de mínima fluidização do leito. Saca só: Δ P L m f = 1 - ε m f ρ s - ρ g

    E: Δ P L m f = 150 . 1 - ε m f 2 ε m f 3 .   μ . q m f ϕ . d v 2 + 1,75 . ( 1 - ε m f ) ε m f 3 . ρ . q m f 2 ϕ . d v

    Vamos calcular desses três jeitos pra ver!

    Passo 2

    Começando pela equação empírica, que é mais simples, pra ir aquecendo os neurônios:

    Δ P ≅ P e s o   d o   l e i t o A

    Como, na fluidização com gás, o peso do sólido é muuuuuito maior que o peso do fluido, podemos aproximar por:

    Δ P ≅ P e s o   d e   s ó l i d o s A

    Daí, adotando SI:

    Δ P = 100   k g   .   9,81   m / s 2 π . 0,30   m 2 4 = 13878,3   P a

    Show!

    Passo 3

    Agora é a vez dessa amiguinha aqui:

    Δ P L m f = 1 - ε m f ρ s - ρ g

    Olhando no enunciado:

    L m f = 1,4   m

    ρ s = 2500   k g / m 3

    A densidade do ar nessas condições nós podemos procurar numa tabela ou calcular considerando que ele se comporte como gás ideal.

    P V = n R T = m M M R T

    ρ a r = m V = P . M M R T

    A massa molar do ar pode ser aproximada por uma média ponderada das massas molares do gás oxigênio ( 32   g / m o l ) e do gás nitrogênio ( 28   g / m o l ). Considerando que o ar seja constituído de 80% de N 2 e 20% de O 2 :

    M M a r = 0,8.28 + 0,2.32 = 28,8 g m o l = 28,8.10 - 3 k g m o l

    Temperatura e pressão são dados no enunciado:

    P = 1   a t m = 1,013.10 5   P a

    T = 500 ° C = 773 K

    E R para o SI é:

    8,31   m 3 . P a . K - 1 . m o l - 1

    Então:

    ρ a r = P . M M R T = 1,013.10 5   .   28,8.10 - 3 8,31   .   773 = 0,454   k g / m 3

    Pra poder usar a equação, só falta a porosidade de mínima fluidização:

    ε m f = V t o t - V s V t o t m f

    O volume de sólido é sempre o mesmo:

    V s = m s ρ s = 100   k g 2500   k g / m 3 = 0,04   m 3

    Já o volume total, depende da nossa altura. Na condição de mínima fluidização:

    V t o t m f = A . L m f = π . 0,3 2 4 . 1,4 = 0,099   m 3

    Então: ε m f = 0,099 - 0,04 0,099 = 0,60

    Daí:

    Δ P L m f = 1 - ε m f ρ s - ρ g

    Δ P 1,4 = 1 - 0,6 2500 - 0,454 . 9,81

    Δ P = 13731,5   P a

    Ligeiramente diferente da que calculamos antes né? Mas tudo bem, porque uma das fórmulas tem uma pegada mais empírica, com simplificações e tal 😊

    E ainda falta a terceira forma de calcular!

    Passo 4

    Agora é a hora desse monstrinho:

    Δ P L m f = 150 . 1 - ε m f 2 ε m f 3 .   μ . q m f ϕ . d v 2 + 1,75 . ( 1 - ε m f ) ε m f 3 . ρ . q m f 2 ϕ . d v

    Vamos listar o que temos pra calcular a queda de pressão:

    L m f = 1,4   m

    ε m f = 0,6

    q m f = 1,61.10 - 2   m / s

    ϕ   =   0,8

    d v = 100.10 - 6   m

    ρ a r = 0,454   k g / m 3

    Só faltou a viscosidade do ar. E aí não tem jeito... tem que procurar tabelado:

    μ a r = 0,035   c P = 0,035.10 - 3   N . s / m 2

    Partiu?

    Δ P 1,4 = 150 . 1 - 0,6 2 0,6 3 .   3,5.10 - 5 . 1,61.10 - 2 0,8   .   100.10 - 6 2 + 1,75 . ( 1 - 0,6 ) 0,6 2 . 0,454 . ( 1,61.10 - 3 ) 2 0,8   .   100.10 - 6

    Δ P 1,4 = 9782,986 + 0,0286032

    Δ P = 13696,2   P a

    Resposta

    Δ P = 13,7   k P a

    Resposta

    Ei, a resposta está no passo a passo :)

    Exercício Resolvido #2

    Elaboração própria

    Calcular a queda de pressão em um leito fluidizado com 2   m de comprimento composto por 150 kg de um material com densidade 2700   k g / m 3 se:

    • fluido utilizado é ar

    Dados:

    • Diâmetro do leito que contém o fluido é D = 0,5   m
    • Porosidade vale ε = 0,4

    Passo 1

    Nessa questão, é só lembrar daquele resultado que vimos na teoria:

    Δ P = P e s o   d o   l e i t o A = P e s o   d e   s ó l i d o s + P e s o   d e   f l u i d o A

    No caso do fluido ser um gás, podemos desprezar o peso do gás e a fórmula se resume a:

    Δ P = P e s o   d o   l e i t o A ≈ P e s o   d e   s ó l i d o s A

    Calculando logo a área transversal do leito, usando o SI:

    A = π . 0,5 2 4 = 0,196   m 2

    Passo 2

    O peso dos sólidos é de boas, já que nos foi dada a massa de sólidos. Usando o SI:

    P e s o   d e   s ó l i d o s = m S . g = 150   .   9,8 = 1470   N

    Daí, usando tudo no SI:

    Δ P ≈ m S . g A = 150   .   9,8 π   .   0,5 2 4 = 1470 0,196 = 7500   P a

    Resposta

    Δ P = 7500   P a

    Exercício Resolvido #3

    Elaboração própria

    Calcular a queda de pressão em um leito fluidizado com 2   m de comprimento composto por 150 kg de um material com densidade 2700   k g / m 3 se:

    • fluido é água

    Dados:

    • Diâmetro do leito que contém o fluido é D = 0,5   m
    • Porosidade vale ε = 0,4
    • ρ á g u a = 1000   K g / m 3

    Passo 1

    Nessa questão, é só lembrar daquele resultado que vimos na teoria:

    Δ P = P e s o   d o   l e i t o A = P e s o   d e   s ó l i d o s + P e s o   d e   f l u i d o A

    SEEEEE o fluido fosse gás, o peso dele seria pequeno, desprezível, mas sendo líquido, teremos que considerar o peso do fluido!

    Já vou calcular logo a área transversal do leito que é bem direto:

    A = π . 0,5 2 4 = 0,196   m 2

    Passo 2

    Dessa vez vamos ter que considerar o peso do fluido na queda de pressão. Daí:

    Δ P = P e s o   d o   l e i t o A = P e s o   d e   s ó l i d o s + P e s o   d e   f l u i d o A

    O peso dos sólidos é de boas, já que temos a massa deles:

    P e s o   d e   s ó l i d o s = m S . g = 150 . 9,8 = 1470   N

    Mas precisamos calcular a massa de fluido ainda e faremos isso usando a porosidade. Sabemos que:

    ε = V o l u m e   d e   v a z i o V o l u m e   t o t a l

    V o l u m e   t o t a l = π . D 2 4 . L = π . 0,5 2 4 . 2 = 0,39   m 3

    Daí:

    0,4 = V o l u m e   d e   v a z i o 0,39   m 3

    V o l u m e   d e   v a z i o = 0,156   m 3  

    O “vazio” é ocupado por fluido, que no caso é água. Sabemos que:

    ρ = m V

    1000 = m 0,156

    m = 156   K g

    Daí:

    p e s o   d e   f l u i d o = 156   .   9,8 = 1528,8   N

    Passo 3

    Agora que temos os pesos de sólidos e fluido, é só juntar tudo:

    P e s o   d e   s ó l i d o s = 150   .   9,8 = 1470   N p e s o   d e   f l u i d o = 156   .   9,8 = 1528,8   N

    Achando o Δ P , usando tudo no SI:

    Δ P = P e s o   d e   s ó l i d o s + P e s o   d e   f l u i d o A = 1470 + 1528,8 0,196 = 15300   P a

    Resposta

    Δ P = 15300   P a

    Exercício Resolvido #4

    UFRJ, Lista 6, Prof. Medronho

    Um leito fluidizado é formado adicionando-se 100 kg de zeólita ( d   =   100   µ m , ρ S   =   2,5   g / c m 3   e   Φ   =   0,8 ) a uma coluna com 30   c m de diâmetro. Como distribuidor de gás, utilizar-se-á uma placa sinterizada de 1   c m de espessura com k   =   10 - 8 c m 2 e ε   =   0,4 . Sabendo-se que o fluido tem as propriedades do ar a 500   ° C   e   1   a t m e que a altura nas condições de fluidização mínima é 125   c m , pede-se:

    1. A velocidade do gás na fluidização mínima.

    Passo 1

    Para saber a velocidade de fluidização mínima, podemos usar aquela expressão que vimos na teoria que vale pra qualquer ponto da fluidização:

    μ K 1 + C K ρ q μ q = 1 - ε ( ρ S - ρ ) g

    Precisamos determinar K ,   C   e   ε m f pra poder calcular q m f ; o μ   e   ρ vamos ter que procurar em tabela pras condições que ele deu.

    Propriedades do ar a 500   ° C   e   1   a t m

    μ = 3,5 . 10 - 4   P o i s e

    ρ = 4,56 . 10 - 3 g c m 3

    No caso do ρ , se não tivéssemos o valor tabelado poderíamos assumir gás ideal e calculá-lo, por exemplo.

    Passo 2

    Bora determinar ε m f logo.

    ε = v o l u m e   d e   " v a z i o " v o l u m e   t o t a l = v o l u m e   t o t a l - v o l u m e   d e   p a r t í c u l a s v o l u m e   t o t a l

    Usando o CGS:

    ε m f = π . ( 30 ) 2 4 . 125 - m p ρ S π . ( 30 ) 2 4 . 125 = 88350 - 100 . 10 3 2,5 88350 = 88350 - 40000 88350 = 0,55

    Agora que temos ε m f , podemos calcular K m f :

    K m f = Φ d - 2 ε m f 3 36 β 1 - ε m f 2 = ( 0,8.100 . 10 - 4 ) 2 . 0,55 3 36.5 . 1 - 0,55 2 = 2,9 . 10 - 7   c m 2

    Para C , temos a correlação de Santana e Massarani:

    C = 0,13 K 0 K 0,37 + 0,10 K 0 K 0,01 0,98 ε - 3 2  

    Em que K 0 = 1 . 10 - 6   c m 2 e essa correlação é válida para valores de K entre:

    K ϵ 1 . 10 - 9   ,   1 . 10 - 3   c m 2

    Daí:

    C m f = 0,13 K 0 K m f 0,37 + 0,10 K 0 K m f 0,01 0,98 ε m f - 3 2 = 0,77

    Usando tudo isso lá naquela equação do passo 1:

    μ K 1 + C K ρ q μ q = 1 - ε ( ρ S - ρ ) g

    3,5 . 10 - 4 2,9 . 10 - 7 1 + 0,77 2,9 . 10 - 7 . 4,56 . 10 - 3 . q 3,5 . 10 - 4 q = 1 - 0,55 2,5 - ( 4,56 . 10 - 3 ) 981

    q = 0,9 1 c m s

    Resposta

    q = 0,9 1 c m s

    Resposta

    Ei, a resposta está no passo a passo :)