Força Resistiva
Produzido por Marcelo AlvesTeoria
Introdução
Nós já sabemos que a velocidade de uma partícula sedimentando em um fluido não vai aumentar infinitamente; ela vai aumentando até que chega em um valor constante, que é a velocidade terminal dela. Vimos lá no tópico de velocidade terminal que isso acontece devido a uma força resistiva ao movimento, que é a força de arraste. Também vimos que essa força de arraste depende do coeficiente de arraste; bora lembrar dele?
O que não vimos ainda é como calcular o valor de , mas vamos ver agora.
Outra coisa que quero te lembrar é que, também da análise dimensional, descobrimos que o depende do número de Reynolds , que é esse aqui oh:
Eu coloquei por causa daquele lance da partícula atingir a velocidade terminal muito rapidamente. Então podemos desprezar a fase acelerada do movimento.
Voltando pra , o lance é que a forma de calcular o varia com o Reynolds também. Mas vou te passar um bizu: existem umas correlações maravilhoooosas que servem pra até números muitooo altos de Reynolds e vamos poder trabalhar APENAS com elas.

Problemas Clássicos
Existem dois tipos de problema que podem aparecer na sua prova e, para cada um deles, você vai ter que usar uma correlação um pouquinho diferente. Então bora ver esses dois casos:
1. Dados e , quero
Vou escrever, agora, a fórmula para e . A de eu sei que é a primeira vez que vou apresentar dessa forma, que vem da análise dimensional também:
Tendo , o diâmetro da partícula, se tivéssemos o valor de ou de , poderíamos isolar e calcular ela. Mas não temos ☹
Mas e se desse pra manipular o e o de forma a eliminar esse que está nos causando problemas? Opa, isso dá pra fazer: temos que fazer . Fica assim:
Temos todas as informações pra calcular , então é isso que iremos fazer. E com esse valor na mão, podemos calcular e separadamente (por meio de correlações), o que vai nos permitir finalmente calcular o .
Vou agora te mostrar o outro caso e depois listo todas as correlações, ok?
2. Dados e , quero d
Da mesma forma, precisamos manipular e , mas agora pra fazer o sumir da nossa equação. Para esse caso aqui, vai ser :
E depois relacionamos isso com o e calculamos o d.
Bora ver como encontramos a partir desses valores calculados então.
Correlações de Coelho e Massarani
Chegou a hora de ver essas correlações que eu falei. Qual usar depende do caso em que você estiver. Por exemplo, se estiver no caso 1 e tiver tido que calcular o , você vai ter que usar a correlação pra que envolve o . Além disso, tem uma correlação para também.
E repara que aparecem e , que tem essas definições aqui:
E essas correlações valem até o , então não precisa se preocupar com o regime de escoamento : )
Duas coisas são muito importantes sobre essas correlações:
- Usar o diâmetro sempre, isto é, diâmetro da esfera de mesmo volume que a partícula.
- As correlações supõem partícula isolada! Ou seja, partícula sozinha.
Mas e se a partícula não estiver isolada? Nesse caso vamos fazer tudo o que fizemos até agora e depois corrigimos o valor encontrado de , usando uns fatores que vamos ver já já.
Correções para a velocidade terminal de esferas isoladas
As correlações consideram uma esfera isolada, sozinha, sem nada por perto, mas, na prática, nem sempre vamos poder considerar isso. Então, bora ver algumas correções:
1. Efeito da concentração
Lembra aquela frase lá da Física de que dois corpos não podem ocupar o mesmo lugar ao mesmo tempo? O sistema partícula-fluido também tem que respeitar isso né. À medida que uma partícula vai sedimentando, o fluido vai “andando” em volta dela, pra cima, e “dando espaço” pra ela descer.
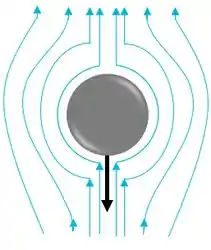
Se a gente tiver mais e mais partículas, o espaço para o fluido passar subindo é menor. Acontece que um mesmo volume de fluido tem que subir, independente do espaço pra ele passar ser grande ou pequeno, e pra compensar a diminuição do espaço pra ele passar, a velocidade dele aumenta.
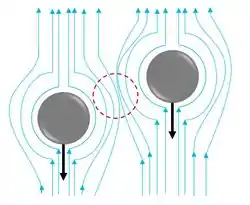
Agora imagina duas situações: a primeira é você andando livremente pela orla de uma praia com um ventinho no seu rosto. A segunda é você tentando sair de um metrô enquanto um mar de pessoas tenta entrar nele correndo. Concorda que é mais difícil você se movimentar quando o que está vindo na direção oposta ao seu movimento está com “mais força”, mais velocidade? A mesma coisa acontece com a partícula...se o fluido que está vindo em direção oposto fica mais rápido, isso representa uma maior força resistiva ao movimento dela e por isso a velocidade terminal dela DIMINUI.
Para calcular a velocidade terminal a uma concentração de partículas , usamos a expressão desenvolvida por Richardson e Zaki:
Em que o valor de é calculado de forma diferente dependendo do :
Com sendo o Reynolds calculado supondo que a esfera está isolada.
E, esclarecendo os termos que aparecem nessa expressão:
A concentração volumétrica calculamos assim:
Algo importante pra dizer é que só vamos usar correção de concentração se .
2. Efeito de Parede
A ideia do efeito de parede é semelhante ao efeito de concentração. Da mesma forma que a presença de outras partículas próximas àquela estudada fazem a diminuir, quando tiver partícula próxima à parede, sobra menos espaço pro fluido subir e isso faz com que a velocidade terminal diminua.
Geralmente desprezamos esse efeito porque a porcentagem de partículas que sedimenta próxima a parede é bem pequena em comparação à quantidade total de partículas precipitando. Mas tem um caso particular que não podemos desprezar por essa porcentagem não ser desprezível: viscosímetro de bola, que tem um efeito lateral simétrico de parede cilíndrica. Vou deixar as equações listadas aqui caso você algum dia precise, mas não vou gastar muito tempo com ele porque não tem nenhuma operação de separação em que esse efeito seja importante.
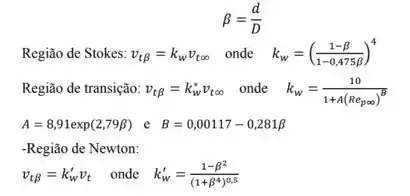
3. Efeito de Stokes-Cunningham
Esse efeito só ocorre em gás! E só é importante quando o diâmetro da partícula é bem pequeno, da mesma ordem de grandeza do livre percurso médio do gás, que é representado por .
Esse livre percurso médio do gás é uma medida da distância média que uma molécula de gás percorre entre um choque e outro com outra molécula de gás. E isso é importante porque o atrito vem de choques da molécula do fluido (que no caso é o gás) com a partícula que está sedimentando, ou seja, precisa ter esse choque pra ter o atrito.
“Mas o que o choque entre moléculas do gás tem a ver com o choque entre molécula do gás e partícula sedimentando?” Então, quando o diâmetro da partícula é da mesma ordem de grandeza do livre percurso médio do gás, a partícula consegue, às vezes, passar entre as moléculas do gás, sem haver choque. E menos choque representam menos atrito, e menos atrito significa que esse efeito AUMENTA .
Vamos então usar um fator para corrigir a velocidade terminal e, como esse efeito aumenta , .
Em que:
Eu sei que as fórmulas são meio tensas, mas uma notícia boa é que embora a teoria desse efeito seja importante e talvez caia em prova, dificilmente vamos considerar esse efeito. Isso porque desprezá-lo é ser conservador uma vez que esse efeito facilita separações, por aumentar .
Se você projetar um equipamento pra um cliente dizendo que ele tem eficiência de e na hora que ele for usar conseguir eficiência de que seja, ele vai te amar...mas se for o contrário, você provavelmente seria demitido.
Mais um detalhe que tenho que falar é o caso de diminuir muitooooo o tamanho da partícula. Aí, não se observa aumento de . O que acontece é que a partícula nem sedimenta.

Calma que eu explico haha. Quando a partícula é muitoooo pequena, ela é tão levinha que sente o choque das moléculas e fica em um movimento aleatório, que chamamos de movimento browniano.

Não resisti haha Movimento browniano não tem nadaaa a ver com brownie mas pelo menos ajuda a lembrar hahah
Diagrama para partículas NÃO-esféricas
Nem todas partículas são esféricas . O que vai acontecer com as não esféricas é que o atrito vai ser maior para elas em comparação com as esféricas e daí o (coeficiente de atrito) vai ser maior pra elas. Um diagrama ficaria mais ou menos como esse aqui embaixo, em que quanto mais pra cima a curva, menor a esfericidade (e maior o para um mesmo ).
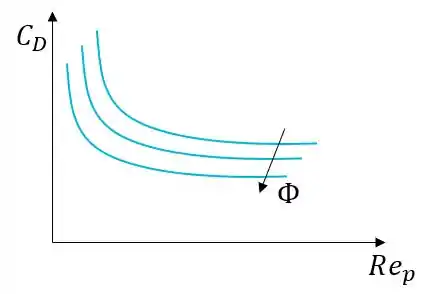
Pra você “visualizar” melhor, pensa numa folha de papel. Se soltarmos ela deitada, ela vai levar um certo tempo pra cair no chão. Agora experimenta amassar ela toda e fazer uma bolinha; vai cair bem mais rápido. A massa da folha é a mesma nos dois casos; o que mudou foi que no segundo a esfericidade era maior.
Correlações de Coelho e Massarani
Correções para a velocidade terminal de esferas isoladas
Diagrama C D v e r s u s R e p para partículas NÃO-esféricas
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria
Calcule a velocidade terminal de uma partícula de hematita com diâmetro de e esfericidade sedimentando em água à .
Dados:
- Densidade da hematita vale
- Utilize, para a água à , e
Passo 1
Bora reunir tudo que sabemos:
O problema pede pra gente calcular a velocidade terminal e nos dá, como informação, e , entre outras coisas. Não vamos querer ficar iterando, então vamos usar as correlações de Coelho e Massarani. Mas qual caminho seguir, ou ? Bora dar uma olhada nas fórmulas:
Repara que temos tudo pra calcular o mas não tudo pra calcular . Daí, vamos por .
Vou adotar o CGS (centímetro-grama-segundo) como sistema de unidades. Todos aqueles nossos dados já estão no CGS, com exceção do diâmetro, mas podemos converter:
Ah, só pra lembrar, Poise é a unidade de viscosidade dinâmica no CGS:
Muuuuuito cuidado na hora de jogar os valores na fórmula para não misturar diferentes sistemas de unidades, ok?
Passo 2
Calculando :
Agora, precisamos usar a correlação para que envolva :
Epa! Não temos nem nem , mas bora calcular:
Agora sim podemos usar a correlação para :
Agora precisamos da definição de Reynolds para achar a velocidade terminal. Lembra que a fórmula que vamos usar direto pra Reynolds é:
Substituindo os valores que temos:
Achamos : )
Resposta
Exercício Resolvido #2
Elaboração própria.
Calcule a máxima velocidade terminal em uma amostra de partículas de sílica, com diâmetros entre e , sedimentando em água à . Considere que a concentração de partículas no fluido é muito baixa.
Dados: e
Passo 1
Temos uma amostra de sílica com diâmetros que variam de a mas que possui esfericidade constante (). O problema pede a máxima velocidade terminal nessa amostra.
O fluido em que as partículas estão sedimentando é água à . Repara que eu não dei dados sobre o fluido no enunciado e isso foi proposital. Na prova, nem sempre você vai ter esses dados diretamente; muitas vezes vai ser que nem nesse enunciado aqui: só diz o fluido e a temperatura dele. Aí, vamos ter que ir atrás de tabelas relacionando temperatura, densidade e viscosidade dinâmica (que é o ) para o fluido em questão. Indo numa dessas tabelas, você vai achar que:
Outro ponto do enunciado que vale a pena ressaltar é quando fala “Considere que a concentração de partículas no fluido é muito baixa.”, que, basicamente, é dizer que não precisa fazer correção de concentração para a velocidade terminal.
Passo 2
Temos que, antes de qualquer coisa, determinar qual é o diâmetro da faixa que tem maior velocidade terminal. Dá uma olhada na fórmula “genérica” de velocidade terminal:
Tanto a área projetada como o volume podem ser escritos como uma constante (que depende da morfologia da partícula) vezes uma potência do diâmetro. Para o volume, essa constante é o fator de forma ; para a área projetada, não tem nenhuma constante específica, então bora dizer que essa constante é .
Daí, simplificando os diâmetros:
Bora comparar as velocidades terminais de duas partículas, e , dessa amostra com . Não sei se as velocidades são=, ou , daí vou usar uma interrogação entre elas:
Tudo que for constante e igual dos dois lados a gente pode cortar.
- Como as partículas possuem mesma morfologia (lembra que essa é uma premissa que sempre usamos para partículas de um mesmo material mesmo se o enunciado não explicitar isso, mas, nesse caso, ele deixou implícito quando deu uma esfericidade só): e .
- Estando as partículas no mesmo fluido, estamos com iguais
- Como estão todas as partículas juntas submetidas a um único campo de forças, é um só
- Como as partículas são do mesmo material, é um só
Daí:
Vimos, lá na teoria, que depende de e , isto é, . Como a morfologia é igual nos dois casos, sobra apenas pra analisar. A fórmula do é
Ou seja, quanto maior , maior o . Agora, lembra lá daquele gráfico :
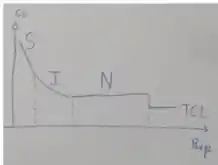
Conforme o aumenta, ou diminuiu ou fica constante, mas nunca aumenta.
- Se :
- Se :
Como :
Daí:
Daí:
Ou seja, a velocidade terminal é sempre maior quanto maior for o diâmetro da partícula, comparando-se partículas de mesmo material e nas mesmas condições. Isso é uma coisa que você tem que saber. Eu demonstrei matematicamente aqui, mas na prova, muito provavelmente, você não vai precisar. Basta lembrar.
Voltando, temos que ver qual é o maior diâmetro da amostra pois é pra ele que temos que calcular a velocidade terminal. E ele é:
Passo 3
Não sabemos qual o regime de escoamento e não queremos ficar iterando então vamos aplicar as correlações de Coelho e Massarani, mas qual caminho seguir, ou ?
Repara que nós temos e ,mas queremos . Daí, vamos por :
Repara que eu joguei todos os valores na fórmula com unidades do CGS (centímetro-grama-segundo). Não podemos misturar sistemas de unidades, hein! Cuidado com isso! Lembrando que o Poise é a unidade de viscosidade dinâmica do CGS.
Como fomos por , para calcular o usamos:
Opa! Não sabemos e . Bora calcular:
Daí:
Usando a definição de :
Resposta
Exercício Resolvido #3
Massarani, G. (2002), Fluidodinâmica em Sistemas Particulados, 2aed
Calcular a velocidade de sedimentação de uma suspensão de partículas em querosene.
Propriedades do fluido: densidade e viscosidade .
Propriedades das partículas: densidade , diâmetro e esfericidade .
Concentração de sólidos na suspensão: .
Passo 1
Bora lá! Temos que calcular a velocidade de sedimentação de partículas. Como vimos que a fase acelerada do movimento é muito curta, vamos considerar desde o início.
O problema dá as propriedades do fluido das partículas: , , , e Vamos usar as correlações de Coelho e Massarani já que não temos informação sobre o regime de sedimentação (Stokes, Newton...) e não queremos ficar 15 anos iterando. Depois de usar as correlações, vamos obter uma velocidade que ainda não é nossa resposta final pois as correlações nos dão um resultado válido para partícula isolada e o enunciado diz que a concentração de sólidos na suspensão é .
Daí, vamos ter que corrigir essa velocidade e achar a velocidade nessa concentração , mas, antes, precisamos converter essa concentração em massa por volume para concentração volumétrica (volume por volume), pois esta que entra na fórmula da correção de Richardson & Zaki:
Em que o valor de do é calculado de forma diferente dependendo do :
Com sendo o Reynolds calculado supondo que a esfera está isolada.
Bora converter logo essa concentração. Vamos adotar como base de cálculo de suspensão, que é o mesmo que . Daí, em de suspensão temos de partículas, que, usando a densidade delas, corresponde a um volume:
Calculando :
Esse é o valor que entra na correção (lembra aquele lance de sempre usar base unitária nas contas?), mas vou passar pra porcentagem só pra te dizer uma coisa:
O que quero te dizer é que realmente vamos ter que usar a correção. Eu passei pra porcentagem porque disse lá na teoria: “Algo importante pra dizer é que só vamos usar correção de concentração se ; caso contrário, podemos desprezá-la.”
Passo 2
Temos e , mas queremos Daí, olhando para os dois possíveis caminhos a seguir:
Temos que ir por porque possuímos todas as informações pra calculá-lo, diferentemente de . Vou adotar o CGS como sistema de unidade porque acho que facilita, então, bora conferir se está tudo no CGS:
Jogando tudo na fórmula de , lembrando que a gravidade () no CGS vale 981:
Como usamos , para achar o temos que usar:
Epa! Cadê e ? Bora calcular!
Jogando na fórmula:
Partindo pra definição de :
Mas não esquece que as correlações de Coelho e Massarani nos dão a velocidade considerando que a partícula está isolada, ou seja, .
Precisamos corrigir essa velocidade considerando o efeito da concentração.
Passo 3
Para corrigir o efeito da concentração e achar a velocidade terminal em uma dada concentração (), usamos a fórmula da correção de Richardson & Zaki:
Como (lembra que é o Reynolds supondo que a partícula está isolada), calculamos por:
Corrigindo, lembrando que calculamos, lá no passo 1,
Resposta
Exercício Resolvido #4
Massarani, G. (2002), Fluidodinâmica em sistemas particulados, 2 ° e d . pág. 35 , Problema 3
Os seguintes dados foram obtidos em ensaios de sedimentação de partículas de em água, a .

A densidade das partículas é e a esfericidade é estimada em .
- Determinar, pela extrapolação de dados, a velocidade terminal das partículas à diluição infinita e, a partir deste valor, calcular o diâmetro das partículas
- Comparar os resultados experimentais com as estimativas segundo a correlação empírica de Richardson & Zaki.
Passo 1
Nessa questão, o enunciado dá pontos relacionando velocidade de sedimentação com concentração de partículas no meio em que elas estão sedimentando. Também nos informa a densidade das partículas e a esfericidade .
Como vimos lá na teoria, quanto maior a concentração, menor a velocidade terminal das partículas sedimentando porque o fluido passando no sentindo oposto ao movimento da partícula fica com maior velocidade, daí gera maior resistência ao movimento. Olhando os dados, estão coerentes com o que esperávamos: quanto maior a concentração, menor .
Temos letras a) e b) pra resolver. Na a), ele pede pra achar à diluição infinita, ou seja, , que seria o caso de partícula isolada, por extrapolação dos dados. Fazemos isso vendo pra como os pontos estão se comportando e assumindo que eles vão seguir a mesma tendência até chegar onde a questão pede, que é . Depois, ele pede pra a partir achar o diâmetro da partícula. Já na b), ele pede pra usar a correlação de Richardson & Zaki e, basicamente, refazer a letra a).
Ah, uma coisa importante: o enunciado diz que o fluido é água a . Daí, vamos ter que ir atrás de uma tabela com propriedades da água em diferentes temperaturas. Olhando nela:
Passo 2
- Determinar, pela extrapolação de dados, a velocidade terminal das partículas à diluição infinita e, a partir deste valor, calcular o diâmetro das partículas
- Comparar os resultados experimentais com as estimativas segundo a correlação empírica de Richardson & Zaki.
Lá no passo 1, disse que extrapolação é ver a tendência dos pontos e assumir que eles vão continuar essa mesma tendência até chegar onde queremos analisar. E a melhor forma de ver essa tendência é jogando os pontos num gráfico:
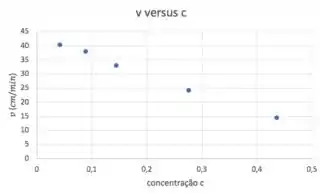
Repara que esses pontos estão mais ou menos alinhados em uma reta, certo? Se você estivesse numa prova (provavelmente estaria fazendo esse gráfico em papel milimetrado), teria que pegar uma régua e traçar a melhor reta para esses pontos. Tipo assim:
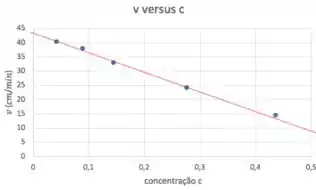
Agora, é só ver, para , qual o valor de Eu diria uns . E não se estressa se você tiver dito , por exemplo. Método gráfico tem muita incerteza mesmo. Só não pode ter dito , por exemplo.
Uma parte já foi, temos . Agora, ainda falta calcular Repara que:
E não temos , daí não podemos calcular e aí não sabemos em qual região estamos (Stokes, Intermediária, Newton ou TCL). Dessa forma, não sabemos qual fórmula usar pra .
Para fugir de iterações, vamos usar as correlações de Coelho e Massarani.
“Ixi, Marcelo! Não lembro quando usar ou usar .” Relaxaaa. Uma dica que eu dou é olhar pro formulário, ver a cara dessas duas expressões e ver as informações que você tem. Olha só:
Para calcular , precisamos de , que é justamente o que não sabemos e queremos calcular. Daí NÃO é essa que vou usar. Mas olha pra agora; temos tudinho : )
Massssss, temos que lançar na fórmula tudo no mesmo sistema de unidades (SI, CGS, sistema inglês etc) pra ser dimensionalmente consistente né. Embora eu adore o SI, aqui na parte de operações unitárias que envolve partículas, na maioria das vezes, é bem conveniente usar o CGS, então vai ser o que você mais vai me ver usando. Bora reunir tudo, convertendo o precisar pro CGS (centímetro-grama-segundo):
Daí:
Agora, obtemos por outra correlação de Coelho e Massarani:
Mas antes precisamos calcular e , sabendo que o enunciado deu :
Substituindo:
Agora sim podemos ir pra definição de , porque só vai sobrar uma variável:
Passo 3
A correlação empírica de Richardson & Zaki é:
Em que o valor de do é calculado de forma diferente dependendo do :
Sendo o Reynolds calculado supondo que a esfera está isolada.
Bora pras contas que vãos entender melhor como usar isso tudo. Vou usar o ponto (.
Precisamos de , que é a concentração volumétrica:
Mas temos uma concentração em massa por volume:
Pra converter, bora adotar uma base de cálculo de de suspensão, que vai ter uma massa de partículas, por regra de três:
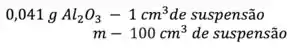
Podemos obter o volume dessa massa já que nos foi dada a densidade das partículas, .
Jogando na fórmula de :
E a velocidade terminal associada a essa concentração é , que é o nosso .
Precisamos do pra continuar e, lá na teoria, eu disse que ele é o Reynolds calculado supondo que a esfera está isolada, ou seja, pega esse e finge que a esfera que tem essa velocidade está isolada, mesmo sabendo que, na verdade, ela NÃO está. Daí, vamos usar o como se ele fosse o . Mas antes, precisamos passar pro CGS, que é o sistema que estamos usando:
Agora sim, com essa velocidade:
Agora, calculando o :
Repara que e NÃO mudaram porque a esfericidade ainda é a mesma.
Como , calculamos por
Daí, calculando , que é a velocidade que relacionaremos, depois, com o tamanho da partícula:
Essa velocidade é um pouquinho diferente da que “achamos” pela extrapolação, que era .
Vamos, agora, calcular o diâmetro da partícula. Vamos, para isso, usar o , que é o associado com esse movimento nessas condições do problema.
Como o enunciado fala para comparar “oS resultadoS”, acho que ele tava querendo que fizéssemos isso para todos os pontos e depois tirássemos uma média dos resultados. Mas ao invés de ficar repetindo várias e várias vezes a mesma coisa, mecanicamente, acho que podemos aproveitar melhor nosso tempo vendo coisas diferentes. Então bora continuar.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #5
Elaboração própria
Determinar o diâmetro da partícula que sedimenta com velocidade , em cada um dos dois casos abaixo:
- Concentração volumétrica de sólidos na suspensão contendo partículas inferior a .
- Concentração volumétrica de sólidos na suspensão contendo partículas é .
Propriedades físicas do fluido: e
Propriedades físicas das partículas: e
Passo 1
Lembra que quanto mais concentrada uma suspensão, menor fica a velocidade terminal das partículas? É isso que vamos trabalhar nessa questão. O enunciado fixa uma velocidade, , e altera a concentração na suspensão. Nosso objetivo é dizer qual é o diâmetro de partícula que vai ter essa velocidade em cada caso.
Na letra a), , daí nos desprezamos a correção do efeito de concentração, porque vai ser muito pequena. (Lembra lá da teoria que só precisamos fazer a correção quando ). Já na b), como , precisamos corrigir! Nesse segundo caso, foi dado , que equivale a (lembra que usamos base unitária nas contas e não porcentagem).
Vou usar o CGS, daí, já vou listar os dados convertendo quando necessário:
Não sabemos o regime de escoamento e não queremos ficar iterando, mas qual caminho seguir: ?
Repara que temos tudo para usar o então é por ele que vamos : )
Passo 2
- Concentração volumétrica de sólidos na suspensão contendo partículas inferior a .
- Concentração volumétrica de sólidos na suspensão contendo partículas é .
Calculando :
Agora, preciso usar isso pra calcular o :
Falta calcular e :
Daí:
Aplicando a formula de :
Convertendo pra , pra deixar o número mais apresentável haha:
Passo 3
Sabemos que quanto mais concentrada uma suspensão, menor fica a velocidade terminal das partículas. Também sabemos que quanto maior a partícula, maior a velocidade terminal dela. Agora, bora juntar essas duas coisas: pensa em uma certa velocidade; conforme você aumenta , você diminui a velocidade terminal das partículas e maior é o diâmetro da partícula que vai ter essa dada velocidade que você fixou. Então, aqui nesse item, já sabemos que vamos achar um diâmetro maior que no item a).
Mas a questão não é teórica, precisamos fazer as contas. O grande lance é que essa velocidade, no item b), é a , já que temos que considerar a concentração (Observação: no item a) dissemos que já que desprezamos o efeito da concentração).
Vamos precisar achar , que é a velocidade que podemos relacionar com o diâmetro. Usando a expressão desenvolvida por Richardson e Zaki:
Em que o valor de do é calculado de forma diferente dependendo do :
Com sendo o Reynolds calculado supondo que a esfera está isolada.
Mas não temos : ( Daí precisamos calcular o . Vamos usar as correlações de Coelho e Massarani, que supõem que a partícula está isolada (ou seja, supõem que esse é o e nos retornam ). Novamente, usamos:
Repara que não mudamos nenhum valor que vamos jogar na fórmula, em relação ao item a), daí o valor é o mesmo:
e só dependem da morfologia (mais especificamente, da esfericidade), que não foi alterada. Daí:
e
Calculando
Novamente, não alteramos nenhum valor em relação ao item anterior:
Ou seja, achamos o valor de por:
Fazendo a correção:
Passo 3
Agora, só falta relacionar com . Vamos ter que, novamente usar .
Finalmente:
Passando pra micra:
Resposta
a)
b)
Exercício Resolvido #6
Elaboração própria
Determinar o diâmetro da partícula que sedimenta com velocidade terminal igual a em ar a e . São conhecidas a densidade e esfericidade da partícula, e , e a viscosidade do fluido,
Passo 1
Essa questão é um pouco diferente das outras que fizemos; aqui, já temos e queremos o diâmetro da partícula que tem essa velocidade. Já ficando de spoiler, vamos usar .
O enunciado dá , e (essa unidade é do SI), mas não deu o ...pelo menos, não diretamente. Mas temos informações sobre o fluido e, a partir delas, conseguimos calcular a densidade dele. (Lá nos exercícios sobre massa especifica fizemos um exercício sobre isso)
Vamos assumir gás ideal (Se o enunciado não falar pra assumir gás real, sempre vamos assumir ideal. E aposto que o enunciado nunca vai pedir gás real haha então nem esquenta a cabeça com isso). Daí, vale:
Em que:
O enunciado já deu que
E deu a temperatura também, mas em graus Celsius, que não é uma escala absoluta.
As escalas absolutas de temperatura são Kelvin e Rankine. Vou escolher converter essa temperatura para Kelvin então:
A temperatura em , que chamei de , vale . Jogando na fórmula, achamos a temperatura em Kelvin, que chamei de :
Ou seja:
Temos agora que manipular o e fazer a densidade aparecer. Olhando a definição de , que é o número de moles:
Substituindo isso na equação dos gases ideiasE agora, a rearranjando:
O enunciado não deu e nem informações pra calcular (Ex: composição do ar atmosférico), daí, temos que ir atrás da informação tabelada (é normal esse tipo de coisa nas questões). Procurando:
Como estamos trabalhando com em , em e em , o que temos que usar é:
Isso também é algo tabelado, né. Calculando :
O é decorrente das unidades que usamos. Mas esse litro aí é bem inconveniente porque não é padrão nem no SI nem no CGS. Vou escolher, nessa questão, trabalhar no SI (bases: Kilo, metro e segundo), então, bora converter essa densidade:
Passo 2
Agora que temos todos os dados, qual caminho seguir?
Repara que não temos mas temos , então é por que vamos. Antes, só falta converter pro SI, já que é esse o sistema que estou usando:
Aí:
Repara que eu usei , já que estamos no SI.
Agora, usamos o para achar :
Falta calcular e :
Daí:
Aplicando a definição de :
Repara que essa unidade está em metros, já que estamos trabalhando no SI. O que o problema pediu já achamos : ) Vou só passar pra por costume mesmo haha