Destilação em Batelada - Múltiplos Estágios – Caso 01
Teoria
Importância desse tópico
Já vimos a destilação em batelada com um único estágio. Agora, veremos a destilação em batelada com múltiplos estágios.
Nesse tipo de destilação com múltiplos estágios, veremos que podem existir dois casos. Nesse tópico, explicaremos os dois, mas só focaremos no primeiro. O primeiro caso é quando temos Razão de Refluxo Constante e, portanto, a vazão de é constante e é variável.
Destilação em batelada com múltiplos estágios
A destilação em batelada em múltiplos estágios vai utilizar uma coluna, pois esses múltiplos estágios farão parte da coluna de destilação.
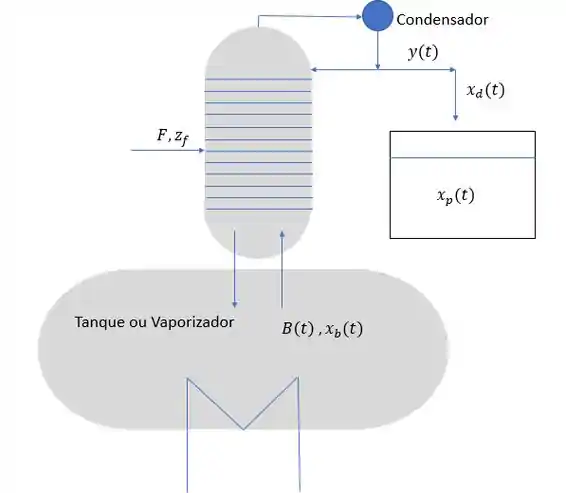
Para a operação de uma coluna com múltiplos estágios, nós precisaremos de uma razão de refluxo, pois precisamos gerar a fase líquida para transferência de massa. A fase vapor é gerada pelo vaporizador. Para isso, teremos duas opções.
A primeira será quando temos Razão de Refluxo Constante e, portanto, a vazão de é constante e é variável. A segunda será uma Razão de Refluxo Variável para ficar constante e, nesse caso,
Destilação em batelada com múltiplos estágios – Caso 01
Para avaliarmos o caso quando temos Razão de Refluxo Constante e, portanto, a vazão de é constante e é variável, precisaremos de umas hipóteses adicionais ( além das que mostramos para batelada com um único estágio).
Vamos assumir uma taxa de vapor constante; que o vapor que deixa a coluna no instante está em equilíbrio com o líquido; vamos desprezar o hold-up do prato ( pois o vaporizador tem um hold up muiiiito maior); e vamos considerar as aproximações realizadas no método Mc-Cabe Thiele.
O hold-up é a quantidade de líquido que fica no prato fazendo a troca.
Bora partir para o Balanço de Massa, lembrando que agora temos também uma carga ( composição ) entrando na coluna.
Balanço de Massa Global
Balanço de Massa por Componente
Abrindo a diferencial, temos que:
Mas, pelo balanço global, vimos que . Então, podemos substituir e organizar nossa equação:
Separando as variáveis:
Mas , então .
Substituindo e reorganizando, temos que:
Integrando, temos que:
Mas relaxa que essa expressão só vai ser usada quando for diferente de zero. E, geralmente, em quase todas as questões . Logo, essa equação fica beeem mais simples.
Essa integral é numérica, ou seja, para ser resolvida precisa utilizar métodos numéricos, como Regra do trapézio, Regra de Simpson, ou qualquer outra que você souber aplicar 😊
Como essa matéria é operações unitárias (e não métodos numéricos), vamos utilizar o mais simples e que também funciona nos exercícios: regra do trapézio. Vou mostrar para vocês nesse caso como eu faria para calcular essa integral, beleza?
Nós queremos calcular a área do que está dentro da exponencial.
Para isso, dividimos a área debaixo da curva em vários “retângulos” pequenininhos e calculamos a área de cada um deles ( base vezes altura). A base é determinada pela diferença dos escolhidos e a altura você calcula o eixo , conforme tá na imagem. No final, é só somar todas as áreas.
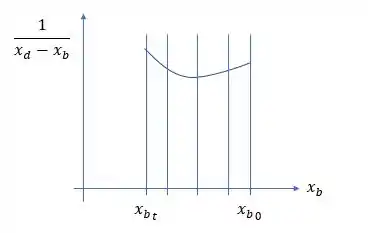
Beleza? Aí substitui o somatório da área que você encontrou na integral!
Cálculo de Tempo de Batelada para destilação em múltiplos estágios ( Caso 01)
Na destilação em múltiplos estágios, também podemos calcular o tempo de batelada. Lembrando que vamos continuar usando as deduções considerando a carga . Para isso, vamos começar integrando essa equação:
Determinação da composição Média - Caso 01
Na destilação em
Dividindo tudo por e reorganizando, temos que:
Isolando e substituindo . Obtemos que:
Portanto, essa é a equação bonitinha que determina o para o caso 01 de destilação em batelada com múltiplos estágios.
Lembrete: Se na questão , simplifica a equação antes de começar a fazer qualquer coisa!!
Destilação em batelada com múltiplos estágios – Caso 01
Cálculo de Tempo de Batelada para destilação em múltiplos estágios ( Caso 01)
Determinação da composição Média x p ( t ) - Caso 01
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria
Indique um dos possíveis casos que ocorrem com a destilação com múltiplos estágios e disserte sobre suas implicâncias.
Passo 1
Falaaa aí!! Tudo joia? Quando falamos sobre destilação com múltiplos estágios temos dois casos possíveis. Sendo que o “Caso 01” que vimos vai ser o mais importante pra gente, certo?
Passo 2
Nesse primeiro caso, temos uma Razão de Refluxo Constante, ou seja,
E isso implica que a vazão de é constante, então, é variável.
Resposta
Um caso é quando temos Razão de Refluxo Constante e, portanto, a vazão de é constante e é variável.
Exercício Resolvido #2
Elaboração própria
Disserte sobre o funcionamento de uma destilação em batelada com múltiplos estágios.
Passo 1
Oi oi oii, vamos relembrar como funciona a destilação em batelada com múltiplos estágios?! Essa destilação vai utilizar uma coluna, pois esses múltiplos estágios farão parte da coluna de destilação. E ai, esquematicamente vamos ficar com:
Lembrando que para um único estágio tínhamos:
Passo 2
Para a operação de uma coluna com múltiplos estágios, nós precisaremos de uma razão de refluxo, pois precisamos gerar a fase líquida para transferência de massa. A fase vapor é gerada pelo vaporizador. Para isso, teremos duas opções.
A primeira será quando temos Razão de Refluxo Constante e, portanto, a vazão de é constante e é variável. A segunda será uma Razão de Refluxo Variável para ficar constante e, nesse caso, Mas esse segundo caso não vai ser tão importante pra gente.
Resposta
Exercício Resolvido #3
Elaboração própria
Quais são as hipóteses que precisamos adotar para o caso em que temos a Razão de Refluxo Constante na destilação em batelada com múltiplos estágios?
Passo 1
Heyyy, antes de vermos as hipóteses específicas para a destilação em batelada com múltiplos estágios vamos dar uma lembradinha em como eram as hipóteses para estágios únicos?
Para destilação em batelada em estágio único tínhamos que:
- O vapor de composição está em equilíbrio com o líquido remanescente no tanque no instante ;
- A taxa de vaporização é constante. Logo, é constante.
Mas porque relembrar disso? Porque essas hipóteses também vão valer para múltiplos estágios 😉
Passo 2
Mas é claro que vamos ter algumas hipóteses a mais. Vamos assumir:
- Taxa de vapor constante;
- O vapor que deixa a coluna no instante está em equilíbrio com o líquido;
- Desprezar o hold-up do prato (pois o vaporizador tem um hold up muiiiito maior);
- Considerar as aproximações realizadas no método Mc-Cabe Thiele, se você não lembra bem dá uma olhadinha lá nesse tópico que pode ser legal 😊.
Ahh, lembrando que o hold-up é a quantidade de líquido que fica no prato fazendo a troca, beleza?
Feshow!
Resposta
As hipóteses são:
- O vapor de composição está em equilíbrio com o líquido remanescente no tanque no instante ;
- A taxa de vaporização é constante. Logo, é constante;
- Taxa de vapor constante;
- O vapor que deixa a coluna no instante está em equilíbrio com o líquido;
- Desprezar o hold-up do prato;
- Considerar as aproximações realizadas no método Mc-Cabe Thiele.
Exercício Resolvido #4
Elaboração própria
Faça o balanço de massa para uma destilação em batelada com múltiplos estágios e Razão de Refluxo Constante considerando
Passo 1
Aaaantes de tudo, precisamos lembrar que nesse caso agora temos também uma carga ( composição ) entrando na coluna. Diferente do que tínhamos em estágio único, beleza? Então o Balanço de Massa Global vai ser:
Passo 2
Já o balanço de massa por componente vai ser:
Podemos ainda abrir a diferencial, ou seja:
Mas, pelo balanço global, vimos que . Então, podemos substituir e organizar nossa equação:
Passo 3
Separando as variáveis, ou seja, tudo que depende de vai para um lado e o que depende de vai para o outro.
Mas , então .
Substituindo e reorganizando, temos que:
Passo 4
Agora podemos integrar,
Essa expressão ta feia, né? Mas ainda bem que vamos considerar . Com isso ficamos com:
Resposta
Exercício Resolvido #5
Destilação diferencial, Problema 1, Universidade Federal do Rio Grande, Escola de Química e Alimentos, Operações Unitárias II, Prof. Roberto G. da Silva
Uma solução aquosa que contém de A e de água é submetida a uma destilação diferencial. Qual o percentual da solução inicial deve ser destilado para que se obtenha um resíduo com de A? Sabendo que a volatilidade relativa média de A em relação à água é .
Passo 1
Bom, antes de tudo vamos entender o que esse enunciado está falando pra gente, beleza? Aqui nós temos uma solução aquosa formada por água e um componente A. Além disso o enunciado nos forneceu:
Repara que o enunciado não nos deu a quantidade da mistura, então vamos utilizar como base de cálculo que,
Além disso, vamos assumir que a solução é ideal, beleza?
E com essas informações nós vamos calcular o percentual da solução inicial que deve ser destilado para que se obtenha um resíduo com . Vamos lá!
Passo 2
Como a mistura é binária e consideramos solução ideal, podemos considerar constante e temos:
Para diferentes valores de obtemos o correspondente e com isso podemos encontrar a equação da linha de equilíbrio.
Então, o que vamos fazer agora é chutar valores de e encontrar a partir da equação de volatilidade relativa.
E com isso, fazendo o ajuste não linear, com auxílio da calculadora, conseguimos extrair a equação da linha de equilíbrio,
Onde o coeficiente de relação é,
Passo 3
Então, o que vamos fazer agora é chutar valores de e encontrar a partir da equação de volatilidade relativa. Por exemplo vamos considerar que,
Então,
Fazendo para vários valores temos,
E com isso, fazendo o ajuste não linear, com auxílio da calculadora, conseguimos extrair a equação da linha de equilíbrio,
Onde o coeficiente de relação é,
Passo 4
Agora nós vamos utilizar a regra do trapézio.
Adequando essa equação ao enunciado temos,
Temos que a área abaixo da curva é numericamente igual ao valor da integral, que vai ser a área de um trapézio.
Passo 5
A destilação vai ocorrer de até e vamos poder traçar um gráfico com eixos .
Então, antes de tudo, vamos construir uma tabela a partir da equação de equilíbrio.
Já com os pontos definidos, podemos traçar o nosso gráfico.
Passo 6
Agora podemos calcular as áreas dos 3 trapézios,
Somando as três áreas, temos,
Que é o valor da integral,
Passo 7
Com isso, utilizando a base de cálculo de temos,
Que é a quantidade de mols que vai ficar dentro do tanque de destilação.
Por diferença, obtemos o percentual da solução inicial que deve ser destilado.
ou
Resposta
ou
Exercício Resolvido #6
Elaboração própria
Calcule o tempo de batelada para uma destilação em múltiplos estágios sabendo que o número de mols no tanque no início da reação era e ao final da destilação tem-se . Dados: e .
Passo 1
Fala aaiii, tudo certinho? Nessa questão queremos calcular o tempo de da destilação em múltiplos estágios, certo? Então vamos usar a fórmula,
E repara que já temos,
Passo 2
Como já temos as informações, precisamos agora substituir na equação,
Resposta
Exercício Resolvido #7
Elaboração própria
Determine a expressão da composição média, de uma destilação em batelada com múltiplos estágios assumindo que .
Dica: Faça o balanço de massa da coluna para chegar na expressão.
Passo 1
Bom, como o enunciado foi muito generoso e nos deu uma dica, vamos começar fazendo o balanço de massa dessa coluna de destilação, beleza?
Com isso,
Ou seja,
Passo 2
Mas o enunciado nos disse que , então podemos facilitar a nossa vida retirando ele da expressão antes de isolar
Agora vamos dividir tudo por e reorganizar,
Passo 3
Lembrando que,
Mas como ,
Agora podemos substituir na expressão e isolar , ficando com: