Destilação em Batelada -Único Estágio
Produzido por Marcelo AlvesTeoria
Importância desse tópico
Até agora nos tópicos anteriores, tudo que vimos foi a destilação contínua. A destilação em batelada será aquela que a coluna não estará ligada a uma corrente com vazão constante, nessa destilação, vai ser colocado na coluna apenas o material que se deseja destilar.
Ela é super utilizada pois é mais fácil ajustar os parâmetros dessa destilação, ela se adapta com vários cenários operacionais e é indicada para operações de separação onde a vazão e a quantidade de produto de topo é pequena e não indica o uso de separação contínua.
Também faremos todas as deduções de destilação batelada usando o método de Mc-Cabe Thiele para misturas binárias, com aproximações.
Nesse primeiro tópico vamos apenas ver destilação em batelada com um único estágio 😊
Destilação em batelada com um único estágio
O tipo mais simples de destilação em batelada é a destilação em batelada com um único estágio. Podemos definir como um tanque ou vaporizador, em contato com um dispositivo de aquecimento, que gerará uma corrente vaporizada. Essa corrente será coletada e sua composição será . O produto final obtido, separado no tanque que coletou o produto condensado ao longo do tempo terá a composição .
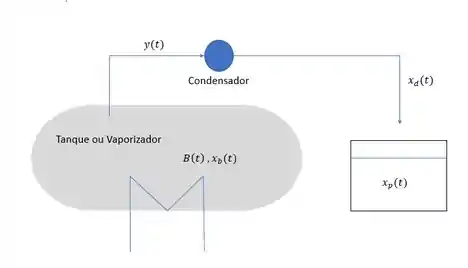
Podemos definir algumas outras variáveis que vão aparecer quando estivermos estudando isso:
é o número de mols de líquido no vaporizador no tanque no instante .
é a composição do líquido no tanque no instante .
é número de mols de líquido iniciado no tanque.
é a composição inicial de líquido no vaporizador.
é a composição do vapor que deixa o pote no instante .
é a composição instantânea do produto de topo no instante .
é a composição média do produto de topo no instante no tanque de produto.
Hipóteses e avaliação da Batelada em único estágio
Para fazer o modelo matemático dessa destilação vamos assumir algumas hipóteses:
A primeira é que o vapor de composição está em equilíbrio com o líquido remanescente no tanque no instante .
A segunda é que a taxa de vaporização é constante. Logo, é constante.
Para fazer o balanço de massa, precisaremos fazer um balanço de massa que varie com o tempo, ou seja, transiente.
Balanço de Massa Global
Balanço de Massa por Componente
Resolvendo a multiplicação dentro da nossa derivada, obtemos que:
Podemos substituir e obter que:
Reorganizando essa equação, obtemos que:
Sabemos que , portanto . Substituindo na equação anterior e reorganizando, obtemos a seguinte equação:
Se integrarmos obtemos que:
Cálculo de Tempo de Batelada para destilação em um único estágio
Ainda na destilação em único estágio, podemos calcular o tempo de batelada. Para isso, vamos começar com integração.
Integrando, temos que:
Como , podemos substituí-lo na expressão do tempo.
E, portanto, essa é a nossa equação para determinar o tempo de batelada 😊
Determinação da composição média
Nós falamos que a composição de varia com o tempo, e, portanto, usamos uma composição média do produto .
Para determinar isso, podemos começar com um balanço de massa:
Lembrando que aí ainda vai precisar substituir o aí dentro, ok?!?
Mistura binária e solução ideal
Como a mistura é binária e consideramos solução ideal, podemos considerar constante e usar a equação que já utilizamos várias vezes ao longo de operações.
Como o condensador utilizado é total, podemos dizer que . Assim, nossa equação de em função de fica um pouquinho diferente:
Assim, resolvendo essa integral, podemos obter uma nova expressão para .