Determinação da Altura da Coluna Recheada
Produzido por Marcelo AlvesTeoria
Análise da coluna
Faaaaala Aíi! Tudo bem? Até agora nós já falamos sobre difusão mássica, diâmetro da coluna e agora vamos conversar sobre a altura dela! Então saca só essa imagem:
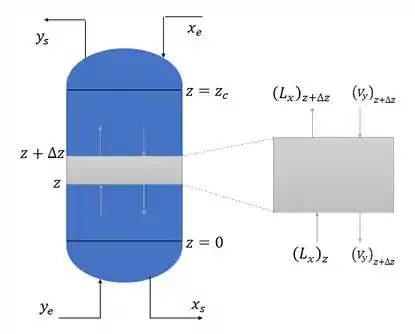
Repara aqui nós vamos começar em uma escala micro e depois para macro, ou seja, vamos analisar um pedaço infinitesimal da coluna (parte cinza) para depois vermos a altura da coluna em si, beleza?
Ahh, e para isso precisamos ter algumas nomenclaturas em mente:
Balanço de Massa
Vamos fazer aqui dois balanços de massa para o soluto, um para a fase vapor e outra para fase líquida olhando para o pedaço infinitesimal da coluna.
Balanço de Massa para o soluto na fase vapor:
Podemos aqui dividir a equação por e aplicar
Com isso obtemos,
Balanço de Massa para o soluto na fase líquida:
Aqui vamos seguir a mesma linha de raciocínio de dividir a equação por e aplicar
Repara que basicamente o que muda é que antes era e agora é dentro da derivada. 😉
Dimensionamento para Destilação
Para isso vamos considerar sistemas binários com vazões molares constantes e assumir que o soluto é o componente mais volátil, beleza?
Manipulando algumas fórmulas, que não vai ser necessário sabermos as etapas na hora da prova, encontramos que a altura da coluna é,
Calma, não se assuste com essa fórmula, normalmente é fornecida para você na hora da prova! \o/
Para simplificar podemos também usar,
Onde é a altura relativa a uma unidade de transferência (FG) e é equacionado como,
Por consequência, que é o número de unidades de transferência da coluna é,
Ahhh e para fase líquida teríamos,
Onde,
Considerações importantes
Em soluções gasosas ideais é equivalente ao número de estágios teóricos e é equivalente a altura do prato teórica,
Além disso, temos também que é igual para as fases vapor/gasosa e líquida, porém, não necessariamente os valores de e dessas duas fases serão idênticos
E também, para fazermos as equações acima assumimos que a transferência ocorre da fase gás para líquida.
Agora partiu exercitar. 😉

Balanço de Massa
Dimensionamento para Destilação
Considerações importantes
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria
Como podemos realizar a análise da altura da coluna?
Passo 1
Heyyy, tudo bem? Para fazer a análise da altura da coluna como um todo precisamos primeiro olhar de uma escala macro para uma escala micro, show?
Passo 2
Então nós vamos analisar um pedaço infinitesimal da coluna (parte cinza que vai da altura até ) para depois vermos a altura da coluna em si.

Resposta
Para analisar a altura da coluna vamos usar um pedaço infinitesimal da coluna para depois vermos a altura real da coluna.
Exercício Resolvido #2
Elaboração própria
Faça o balanço de massa do soluto para uma coluna de destilação recheada.
Passo 1
Oi oi oieee, tudo certinho? Temos a seguinte coluna:

E vamos fazer aqui dois balanços de massa para o soluto, um para a fase vapor e outra para fase líquida olhando para o pedaço infinitesimal da coluna, beleza?
Passo 2
Balanço de Massa para o soluto na fase vapor:
Podemos aqui dividir a equação por e aplicar
Com isso obtemos,
Passo 3
Balanço de Massa para o soluto na fase líquida:
Aqui vamos seguir a mesma linha de raciocínio de dividir a equação por e aplicar
Resposta
Balanço de Massa para o soluto na fase vapor:
Balanço de Massa para o soluto na fase líquida:
Exercício Resolvido #3
Elaboração própria
Que simplificações podemos tirar de soluções gasosas ideais?
Passo 1
Oi oi oieee, tudo certinho? Em soluções gasosas ideais é equivalente ao número de estágios teóricos e é equivalente a altura do prato teórica,
Passo 2
Além disso, temos também que é igual para as fases vapor/gasosa e líquida, porém, não necessariamente os valores de e dessas duas fases serão idênticos
Resposta
E é igual para as fases vapor/gasosa e líquida.