Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Determinação do Número de estágios mínimos

Ver Todos os Exercícios

Teoria

Importância desse tópico

Nesse tópico veremos como determinar o número de estágios mínimos da coluna de destilação e realizar o cálculo dos componentes não chaves. 😊

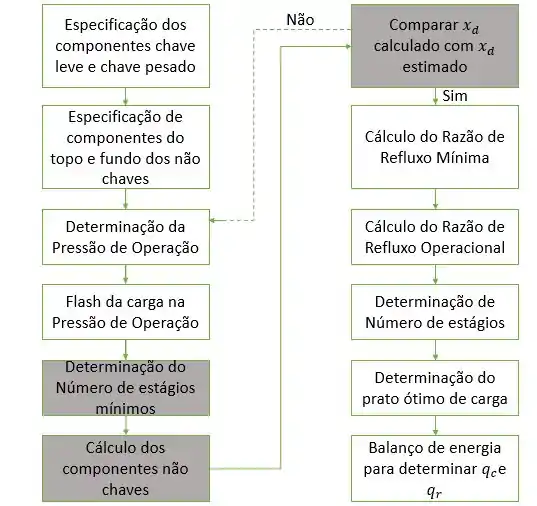
Determinação do número de estágios mínimos

O número de estágios mínimos é obtido quando estamos considerando refluxo total. Nessas condições, a vazão das correntes de líquido e vapor que se cruzam são iguais, já que nenhum produto está sendo gerado. Para calcular esse número de estágios mínimos, aplicamos a equação de Fenskie.

N m í n i m a = ln ⁡   x D , L K x D , H K ∙ x B , H K x B , L K   ln ⁡ α L K , H K -

Onde x D e x B são as composições dos produtos de fundo e de topo dos componentes chave leve (LK) e chave pesada (HK). Já o alfa é a volatlidade relativa média entre esses dois componentes.

O alfa médio é uma média entre o alfa calculado no topo, fundo e carga. Ele fica com essa fórmula aqui:

α L K , H K - = α t o p o ∙ α f u n d o ∙ α c a r g a 1 / 3  

Ele vai ser calculado pela divisão do k L K de cada componente dividido pelo k r e f e r ê n c i a , que é o k H K .

Chute inicial dos Componentes não chave

A próxima etapa é o cálculo da composição dos componentes não chave pela Equação de Fenskie. Para isso, vamos precisar aplicar as quatro equações a seguir. Nós vamos ilustrar como aplicar com um exemplo, ok?

d i = d r b r ∙ α i , r - N m i n ∙ f i 1 + d r b r ∙ α i , r - N m i n

d r b r = d H K b H K

x D = d i D

x b = b i / B

Vamos supor que temos uma mistura de 20   m o l / h de C 3 , 30   m o l / h de C 4 , 25   m o l / h de C 5 e 25   m o l / h de C 6 . E nessa mistura o N m í n i m o já foi previamente calculado e é 6,54 . Nessa destilação, deseja-se que o produto de topo possua no máximo 5 % do C 5 alimentado e o produto de fundo 3 % de C 4 alimentado. Portanto, o componente chave pesada é o C 5 .

Nós vamos dizer que o componente chave pesada é o de referência, e tudo que aparece com o r na fórmula se refere a ele. Portanto ele é a referência e seu alfa será igual a 1,00 , pois é a divisão do seu k i pelo k r e f e r ê n c i a , que são a mesma coisa. O alfa médio para os três componentes foi calculado como 7,41 para o C 3 , 2,67 para o C 4 , 1,00 para o C 5 e 0,4 para o C 6 . Lembrando que nesse caso o alfa será:

α i , r = k i k r

Nós precisaremos começar organizando os nossos dados numa tabela do mais volátil para o menos volátil. As colunas em branco são aquelas que precisaremos completar:

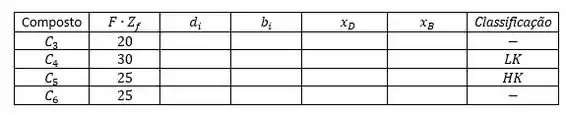
Vamos começar calculando a quantidade de C 5   no produto de topo, considerando a informação que o produto de topo possui no máximo 5 % do C 5 alimentado.

d C 5 = 0,05 ∙ 25 = 1,25   m o l / h

Logo, b C 5 = 25 - 1,25 = 23,75   m o l / h .

A tabela fica assim então:

Nós vamos estimar que C 3 não sai no produto de fundo e que C 6 não sai no produto de topo.

Precisamos completar com as colunas que faltam. Para isso, basta dividir o d i e b i de cada componente por D e B , respectivamente. Sendo que D = 20 + 29,1 + 1,25 = 50,35   m o l / h e B = 0,9 + 23,75 + 25 = 49,65   m o l / h .

x D = d i D

x b = b i / B

E aí obtemos essa tabela aqui:

Confirmação dos Componentes não chave

Agora, vamos confirmar se a nossa estimativa estava certa, ok? Para isso, começaremos calculando d r b r :

d r b r = d H K b H K = 1,25 23,75 = 0,06

Vamos mostrar um exemplo de como calcular o d i para o C 3 e aí você tenta para o C 6 , beleza?

d i = d r b r ∙ α i , r - N m i n ∙ f i 1 + d r b r ∙ α i , r - N m i n = 0,06 ∙ 7,41 6,54 ∙ 20 1 + 0,06 ∙ 7,41 6,54 = 19,999   ( q u a s e   20 )

b i = 20 - 19,999 = 0,001   ( b a s i c a m e n t e   z e r o )

Preenchendo essas informações na tabela, vemos que só ficará faltando o cálculo de x D e x B .

Novamente, basta dividir o d i e b i de cada componente por D e B , respectivamente. Sendo que D = 20 + 29,1 + 1,25 = 50,35   m o l / h e B = 0,9 + 23,75 + 25 = 49,65   m o l / h .

x D = d i D

x b = b i / B

E aí obtemos essa tabela aqui:

E essa tabela é igualzinha a anterior, então nosso chute se confirmou!! Caso não tivesse dado igual, precisaríamos voltar e recalcular a pressão de operação ☹

Chute inicial dos Componentes não chave

Confirmação dos Componentes não chave

Exercícios Resolvidos

Exercício Resolvido #1

Elaboração própria

Quais são os dois passos posteriores que devemos tomar após a determinação do número de estágios mínimos?

Passo 1

Antes vamos relembrar tudo que acontece antes de determinarmos o número de estágios mínimos, beleza? Vimos,

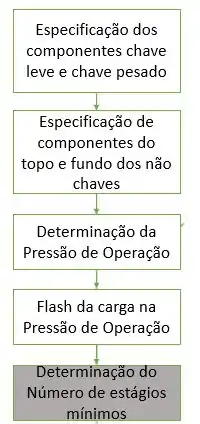
Passo 2

Depois disso o que vamos fazer é calcular os componentes não chaves e comparar o valor de x d calculado com o valor de x d estimado! 😊

Resposta

Calcular os componentes não chaves e comparar o valor de x d calculado com o valor de x d estimado.

Exercício Resolvido #2

Adaptada - Lista de Operações Unitárias I 2018, UFF, Professor Jorge

Calcule o número mínimo de estágios utilizando a equação de Fesnkie sabendo que deseja-se ter 75 % da espécie A (chave-leve) e 11 %   da espécie B (chave-pesada) na corrente de topo e 33 % da espécie B e 27 %   da espécie A na corrente de fundo. Sabendo que α A , B = 1,33 .

Passo 1

Nessa questão o enunciado está nos pedindo para calcular o número de mínimo de estágios com a equação de Fenskie, ou seja,

N m í n i m a = ln ⁡   x D , L K x D , H K ∙ x B , H K x B , L K   ln ⁡ α L K , H K -

Sendo que ele já indicou que,

L K → A

H K → B

Então, vamos lá!

Passo 2

Do enunciado vemos que a composição da corrente de topo é,

x D , L K = 0,75

x D , H K = 0,11

Da mesma maneira nos foi dado que,

x B , L K = 0,27

x B , H K = 0,33

Passo 3

Agora podemos substituir as informações anteriores na nossa fórmula e encontrar,

N m í n i m a = ln ⁡   0,75 0,11 ∙ 0,33 0,27   ln ⁡ 1,33

N m í n i m a = 2,120 0,285 = 7,43

Opaaa, nós não temos como ter um número de estágios quebrado, né?

Então aqui vamos utilizar apenas números inteiros arredondando para cima para dar aquela famosa margem de segurança. Logo,

N m í n i m a = 8,0

Resposta

N m í n i m a = 8,0

Exercício Resolvido #3

Adaptada - Lista de Operações Unitárias I 2018, UFF, Professor Jorge

Calcule o número mínimo de estágios utilizando a equação de Fesnkie sabendo que deseja-se ter 75 % da espécie A (chave-leve) e 11 %   da espécie B (chave-pesada) na corrente de topo e 33 % da espécie B e 27 %   da espécie A na corrente de fundo. Sabendo que α A , B = 1,5

Passo 1

Nessa questão o enunciado está nos pedindo para calcular o número de mínimo de estágios com a equação de Fenskie, ou seja,

N m í n i m a = ln ⁡   x D , L K x D , H K ∙ x B , H K x B , L K   ln ⁡ α L K , H K -

Sendo que ele já indicou que,

L K → A

H K → B

Então, vamos lá!

Passo 2

Do enunciado vemos que a composição da corrente de topo é,

x D , L K = 0,75

x D , H K = 0,11

Da mesma maneira nos foi dado que,

x B , L K = 0,27

x B , H K = 0,33

Passo 3

Agora podemos substituir as informações anteriores na nossa fórmula e encontrar,

N m í n i m a = ln ⁡   0,75 0,11 ∙ 0,33 0,27   ln ⁡ 1,5

N m í n i m a = 2,120 0,405 = 5,22

Repara aqui se fossemos arredondar, normalmente arredondaríamos para 5 , 2 , certo? Mas nós não temos como ter um número de estágios quebrado.

Então aqui vamos utilizar apenas número inteiros arredondando para cima para dar aquela famosa margem de segurança. Logo,

N m í n i m a = 6

Feshow! 😉

Resposta

N m í n i m a = 6

Exercício Resolvido #4

Elaboração própria

Calcule o alfa médio sabendo que o componente chave leve é A e que o componente chave pesada é B.

Dados:

T o p o → k A = 14,0 ;   k B = 7,0

F u n d o → k A = 4,0 ;   k B = 9 , 0 ;   k c = 4,0

C a r g a → k A = 15 , 0 ;   k B = 11 , 0 ;   k c = 4,0

Passo 1

Para calcular o alfa médio precisamos primeiro calcular o alfa de cada componente da coluna como indicado na equação,

α L K , H K - = α t o p o ∙ α f u n d o ∙ α c a r g a 1 / 3  

Onde cada α   vai ser calculado pela divisão do k L K de cada componente dividido pelo k r e f e r ê n c i a , que é o k H K .

Passo 2

Vamos começar calculando o α t o p o ,

α t o p o = k L K k H K = k A k B = 14,0 7,0 = 2

Agora no fundo α f u n d o ,

α f u n d o = k L K k H K = k A k B = 4,00 9 , 0 = 0,44

E por última na carga, ou seja, na alimentação da coluna α c a r g a ,

α t o p o = k L K k H K = k A k B = 1 5 , 0 11 , 0 = 1,36

Passo 3

Agora podemos substituir na expressão do Passo 1 😉

α L K , H K - = 2 ∙ 0,4 ∙ 1,36 1 / 3  

α L K , H K - = 1,088 1 / 3

α L K , H K - = 1,03

Feshow!

Resposta

α L K , H K - = 1,03

Exercício Resolvido #5

Adaptado - Multicomponente, Lista de Operações Unitárias II, Profa. Silvia, Escola de Química UFRJ, EQE-482

Uma torre de fracionamento deve ser projetada para processar uma mistura com 500   m o l / h , líquida saturada contendo 30   m o l % de n-butano, 30   m o l % de n-pentano, 20   m o l %   d e   n-hexano e 20   m o l %   d e   n-heptano. Este líquido deve ser processado de modo a recuperar 95 % do n-pentano no destilado a 98 %   do n-hexano no resíduo. Determine o número mínimo de estágios sabendo:

α t o p o = 2,83 , α f u n d o = 2,73 e α c a r g a = 2,24

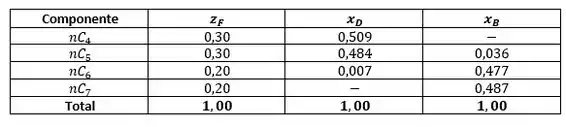
Passo 1

Falaaa ai, tudo bem? Nessa questão nós queremos calcular o número mínimo de estágios. Mas para isso precisamos calcular primeiro o valor do alfa médio com,

α L K , H K - = α t o p o ∙ α f u n d o ∙ α c a r g a 1 / 3

E depois disso podemos calcular o número de estágios mínimos com,

N m í n i m a = ln ⁡   x D , L K x D , H K ∙ x B , H K x B , L K   ln ⁡ α L K , H K -

Passo 2

Começando pelo cálculo do alfa médio, podemos substituir os valores do alfa do topo, fundo e carga na fórmula,

α L K , H K - = α t o p o ∙ α f u n d o ∙ α c a r g a 1 / 3

α L K , H K - = 2,83 ∙ 2,73 ∙ 2,24 1 / 3

α L K , H K - = 2,59

Agora podemos seguir para a segunda parte!

Passo 3

Mas antes de substituir esses valores na equação para encontrar o número mínimo de estágios, precisamos identificar quem é chave leve e quem é chave pesada.

Lembrando que chave leve é o mais pesado dos leves que sai no produto de fundo e chave pesada e o mais leve dos pesados que sai no produto de topo. De acordo com as especificações de recuperação do enunciado temos,

n C 5 → recuperação de 95 % no destilado = 5 % no fundo (chave leve)

n C 6 → recuperação de 9 8 % no destilado = 2 % no fundo (chave pesada)

Passo 4

Agora que identificamos quem é o chave leve e quem é o chave pesada podemos substituir os valores na equação a partir dos valores da tabela no enunciado.

N m í n i m a = ln ⁡   x D , L K x D , H K ∙ x B , H K x B , L K   ln ⁡ α L K , H K - = ln ⁡   0,484 0,036 ∙ 0,477 0,007   ln ⁡ 2,58

N m í n i m a = 7,2

Logo, o número mínimo de estágios é 8.

Resposta

N m í n i m a = 8

Exercício Resolvido #6

Elaboração própria

Vamos supor que temos uma mistura de 30   m o l / h de C 3 , 40   m o l / h de C 4 , 20   m o l / h de C 5 e 15   m o l / h de C 6 . E nessa mistura o N m í n i m o já foi previamente calculado e é 7,00 . Nessa destilação, deseja-se que o produto de topo possua no máximo 5 % do C 5 alimentado e o produto de fundo 3 % de C 4 alimentado. Determine valores para x D .

Passo 1

Antes de tudo precisamos identificar quem é o componente chave leve e quem é o componente chave pesada. Como deseja-se que o produto de topo possua no máximo 5 % do C 5 alimentado e o produto de fundo 3 % de C 4 alimentado, o componente chave pesada é o C 5 .

O componente chave pesada é o de referência. Portanto seu alfa será igual a 1,00 , pois é a divisão do seu k i pelo k r e f e r ê n c i a , que são a mesma coisa. O alfa médio para os três componentes foi calculado como 7,41 para o C 3 , 2,67 para o C 4 , 1,00 para o C 5 e 0,4 para o C 6 . Lembrando que nesse caso o alfa será:

α i , r = k i k r

Passo 2

Nós precisaremos começar organizando os nossos dados numa tabela do mais volátil para o menos volátil. As colunas em branco são aquelas que precisaremos completar:

Vamos começar calculando a quantidade de C 5   no produto de topo, considerando a informação que o produto de topo possui no máximo 5 % do C 5 alimentado.

d C 5 = 0,05 ∙ 20 = 1 , 00   m o l / h

Logo, b C 5 = 2 0 - 1 , 00 = 19,00   m o l / h .

A tabela fica assim então:

Passo 3

Agora nós vamos estimar que C 3 não sai no produto de fundo e que C 6 não sai no produto de topo, ou seja,

Precisamos completar com as colunas que faltam. Para isso, basta dividir o d i e b i de cada componente por D e B , respectivamente. Sendo que D = 3 0 + 38,8 + 1 , 0 = 69,80   m o l / h e B = 1 , 2 + 19,0 + 15 = 3 5 , 2   m o l / h .

x D = d i D

x b = b i / B

E aí obtemos essa tabela aqui:

Resposta

Exercício Resolvido #7

Elaboração própria

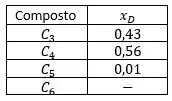
Vamos supor que temos uma mistura de 30   m o l / h de C 3 , 40   m o l / h de C 4 , 20   m o l / h de C 5 e 15   m o l / h de C 6 . E nessa mistura o N m í n i m o já foi previamente calculado e é 7,00 . Nessa destilação, deseja-se que o produto de topo possua no máximo 5 % do C 5 alimentado e o produto de fundo 3 % de C 4 alimentado. Confirma se a estimativa de x d abaixo está correta dado α i , r - N m i n = 7,41

Passo 1

Falaaaa aí, tudo show de bola? Nessa questão já nos foi dado o valor chutado de x d e precisamos confirmar se está certinho, beleza? Para isso, precisamos começar calculando d r b r .

d r b r = d H K b H K

A partir disso podemos encontrar o valor de d i com a equação,

d i = d r b r ∙ α i , r - N m i n ∙ f i 1 + d r b r ∙ α i , r - N m i n

E comparar com o que temos, show? Vamos lá!

Passo 2

Substituindo os valores na primeira equação temos,

d r b r = d H K b H K = 1 , 00 19,00 = 0,0 5

Agora vamos calcular o d i para o C 3 ,

d i = d r b r ∙ α i , r - N m i n ∙ f i 1 + d r b r ∙ α i , r - N m i n = 0,0 5 ∙ 7,41 7,00 ∙ 3 0 1 + 0,0 5 ∙ 7,41 7,00 = 2 9,999   ( q u a s e   3 0 )

b i = 3 0 - 2 9,999 = 0,001   ( b a s i c a m e n t e   z e r o )

Vamos seguir esse mesmo raciocínio para os outros componente. Com isso ficamos com,

Passo 3

A partir da tabela acima vemos que só ficará faltando o cálculo de x D e x B .

Nesse caso, basta dividir o d i e b i de cada componente por D e B , respectivamente. Sendo que D = 30 + 38,8 + 1,0 = 69,80   m o l / h e B = 1,2 + 19,0 + 15 = 35,2   m o l / h .

x D = d i D

x b = b i / B

E aí obtemos essa tabela aqui:

Como essa tabela é igual a do enunciado, então a estimativa está correta!

Resposta

A estimativa está correta.

Exercício Resolvido #8

Elaboração própria

O que precisamos fazer caso nosso chute inicial para x d não funcione?

Passo 1

Se depois de todas as contas o nosso x d não der certo o que vamos fazer? Sentar e chorar?

Não!!

Passo 2

Caso o valor do nosso x d calculado não tivesse dado igual ao nosso chute inicial nós precisaríamos voltar e recalcular a pressão de operação. Lembra do esquema,

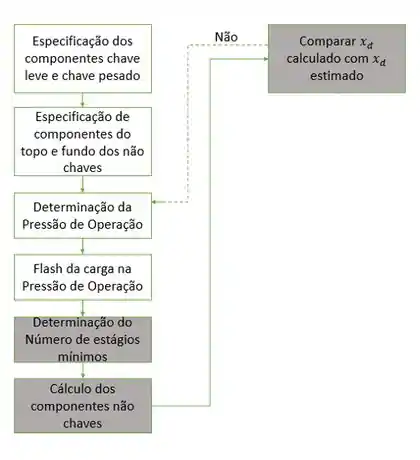
Resposta

Precisaríamos voltar e recalcular a pressão de operação.